Обоснование применения методов математической статистики в гидрологии.
Сток рек меняется из года в год. В этих колебаниях нет строгой закономерности. Вместе с тем величина годового стока колеблется около некоторой средней величины, причем амплитуды таких колебаний неодинаковы в различных физико-географических районах. Между величинами годового стока за два смежных года зависимость практически отсутствует. Такие величины в математической статистике называются случайными величинами, а ряд, образованный ими, вариационным рядом. К изучению случайных величин можно применять методы математической статистики. Применение статистических методов в гидрологии имеет некоторые особенности, обусловленные специфичностью рассматриваемых в гидрологии явлений.
Первая из них заключается в том, что формирование стока рек связаны сложным переплетением непрерывно изменяющихся во времени и в пространстве факторов, что придает величине речного стока вероятностный характер. К числу таких факторов прежде всего относятся климат (осадки, испарение и тепло), почвенно-геологические условия, распространение озер, болот и леса на территории бассейна. Особенно велика роль климатических факторов. Влияние неклиматических факторов тем сильнее, чем меньше размеры бассейна и чем короче период, за который рассматривается это влияние. Эти факторы сказываются как на величины годового стока, так и на его режиме. Причем действие этих факторов проявляется в различных направлениях и вместе с тем эти факторы находятся в постоянном взаимодействии.
Вторая из них заключается в том, что в нашем распоряжении имеется ограниченная информация, которая обычно не может быть существенно увеличена. В связи с этим особую важность приобретают вопросы приведения коротких гидрологических рядов и их статистических параметров к длительному периоду, -экстраполяции различных кривых распределения за пределы данных измерений.
Третья особенность состоит в том, что ряды измерения речного стока нередко могут оказаться неоднородными как во времени так и в пространстве. Это значительно сужает возможность и осложняет статистическое описание совокупностей гидрологических величин. Чаще всего нарушение однородности рядов стоковых характеристик связано с хозяйственной деятельностью на водосборе.
Четвертая особенность применения статистических методов в гидрологии связана с наличием внутрирядной связанности, которая нарушает принцип случайности, в результате чего объем независимой информации, заключающейся в том или ином гидрологическом ряду, уменьшается.
В соответствии с изложенным наряду с генетическим методом в гидрологии широкое распространение получили статистические методы. Следует отметить, что если генетические методы при изучении закономерностей формирования речного стока опираются на физико-математические методы. то статистические методы рассматривают гидрологические процессы как случайные (стохастические) и опираются на математическую статистику.
Основные характеристики стока. Годовой сток может быть выражен в виде расхода Q, объема W, модуля M и слоя стока Y. Расход воды (Q, м3/с) - количество воды в м3, протекающее через поперечное сечение русла в единицу времени (секунду). Различают: мгновенный расход на какой либо момент года; средний расход за заданный период времени (суточный, пентадный, декадный, месячный ,годовой).
В гидрологических расчетах используют следующие статистические параметры расхода воды.
Среднеарифметическое (Q0), характеризующее положение центра, вокруг которого колеблются отдельные значенияQi рассматриваемого ряда расхода воды.
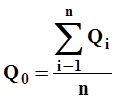
| (1) |
где n - число членов ряда.
Среднеквадратическое отклонение sQo , характеризующее меру рассеяния (отклонения) отдельных значений ряда от среднеарифметического, имеет такую же размерность, что и члены ряда. Имеет следующий вид
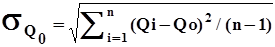
| (2) |
Коэффициент вариацииСv , характеризующий относительную (в долях среднеарифметического) меру изменчивости ряда:
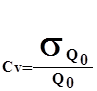
| (3) |
Он является безразмерной характеристикой изменчивости статистической совокупности.
Для оценки степени точности среднего многолетнего значения стока вычисляется средняя квадратическая ошибка средней многолетней величины ряда по формуле
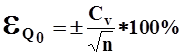
| (4) |
При наличии внутри рядных связей
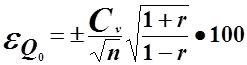 % (5)
% (5)
r - коэффициент корреляции между смежными членами; Сv - коэффициент вариации.
Длина ряда считается достаточной для определения Q0 если eQ0£ 5-10%
Относительная средняя квадратическая ошибка коэффициента вариации
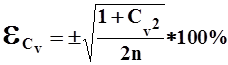
| (6) |
длина ряда считается достаточной для определения 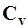 если
если 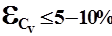 .
.
Если коэффициент вариации устанавливается с помощью метода наибольшего правдоподобия, то
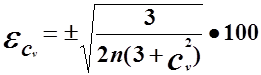 % (7)
% (7)
В гидрологических расчетах кроме расходов воды (Qi), применяется еще модульный коэффициент, который представляет собой отношение расхода(Qi) или стока (Wi) за какой-либо период к среднемноголетнему значению его за тот же период,
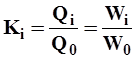
| (8) |
При выражении отдельных членов ряда Wi или (Qi) в виде безразмерных модельных коэффициентов параметр Сv определяется по формуле
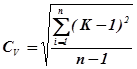  
|  (9)
(9)
|
Коэффициент асимметрииСs ,характеризующий «форму» распределения случайных значений Qi ( или Wi). является безразмерной величиной.
Ряд является симметричным, если положительные и отрицательные отклонения членов ряда от среднего арифметического Q0 повторяется одинаково часто.
В тех случаях, когда положительные отклонения повторяются реже. чем отрицательные, или наблюдается обратное соотношение, ряд - несимметричный (асимметричный).
Коэффициент асимметрииСs рассчитывают по одной из следующих формул:
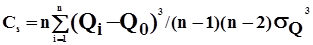 или
или
| (10) |
 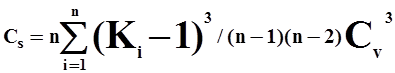
| (11) |
Относительная средняя квадратическая погрешность 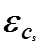 %
%
коэффициента асимметрии по формуле С.Н. Крицкого и М.Ф.Менкеля
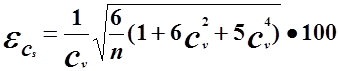 % (12)
% (12)
или же по следующей более простой эмпирической формуле
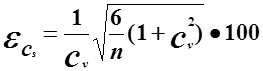 % (13)
% (13)
Влиянием связанности ряда в первом приближении можно в формуле (6) - (13) пренебречь .
Коэффициент автокорреляции r - характеризует статистическую связь между смежными значениями ряда наблюдений Qi и Qi+1. Его определяют по формуле.
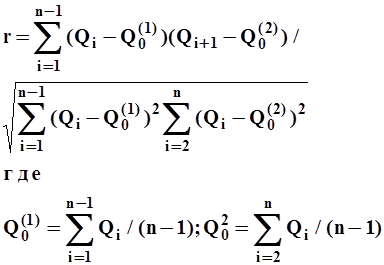
| (14) |
Стандарт погрешности 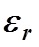 % коэффициента корреляции r между смежными членами ряда
% коэффициента корреляции r между смежными членами ряда
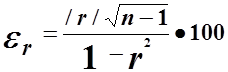 % (15)
% (15)
Средний многолетний объем стока W м3/год - количество воды, стекающее с водосбора за год (можно вычислить за сутки, декаду, месяц и т.п.).
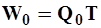
| (16) |
где Т - число секунд в году; Т=86400 *365 = 31,54 106
Cредний многолетний модуль стокаМ0 л/(с км2) - количество воды в литрах, стекающее в секунду с квадратного километра площади водосбора, - определяется по формулам:
 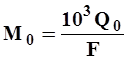
| (17) |
Из формулы (17) можно получить
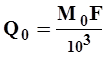
| (18) |
Средний многолетний объем стока можно выразить через модуль стока
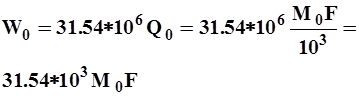
| (19) |
Средний многолетний слой стока Y0(мм) за любой период времени можно вычислить по формуле
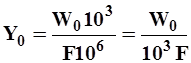 мм/год мм/год
| (20) |
Между слоем и модулем стока существует зависимость
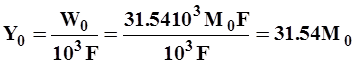
| (21) |
Коэффициент стокаh = 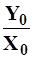 , где Y0-средний многолетний сток, X- средняя многолетняя сумма осадков за год, выпадающих в пределах данного бассейна, заменяя в этой формуле величину Y0 равной ей величиной
, где Y0-средний многолетний сток, X- средняя многолетняя сумма осадков за год, выпадающих в пределах данного бассейна, заменяя в этой формуле величину Y0 равной ей величиной
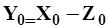
| (22) |
где Z0 потерь осадков на водосборе и прежде всего затрата части осадков на испарение получим,
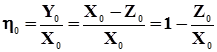
| (23) |
Из формулы (23) следует. что коэффициент стока зависит от годовой суммы осадков и тех факторов, от которых зависит величина потерь Z0. Следует отметить, что с увеличением осадков (X0) дробь 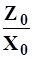 уменьшается, а следовательно, коэффициент стока растет. Коэффициент стока показывает, какая часть осадков превращается в сток.
уменьшается, а следовательно, коэффициент стока растет. Коэффициент стока показывает, какая часть осадков превращается в сток.
Норма годового стока. Количество воды, стекающего с данного бассейна за год, называют годовым стоком. Как отметили в предыдущем разделе годовой сток непрерывно колеблется в зависимости от климатических и физико-географических факторов. Длительными наблюдениями установлено, что колебания годового стока носят циклический характер, выражающийся в последовательной смене многоводных и маловодных лет. Среднюю арифметическую величину годового стока, вычисленную за длительный период, включающий в себя одинаковое число многоводных и маловодных периодов, принято называть нормой стока. Предполагается, что норма стока представляет собой устойчивую величину, т.е. среднеарифметическое значение ее, вычисленное за достаточно длительный период, остается постоянным независимо от прибавления новых членов к вариационному ряду годовых расходов. Однако понятие устойчивости нормы стока и предположение об отсутствии связи между величинами стока за два смежных года является условным.
Распределение нормы стока на территории России таково. Слой стока уменьшается с севера на юг и с запада на восток, так как в этом направлении снижается увлажненность территории и повышается континентальность климата. Для характеристики распределения стока на любой территории строятся карты стока. Карты стока строятся для нормы годового стока, стока за период половодья и т.п.
Определение нормы годового стока по многолетнему ряду наблюдений. При определении нормы стока возможны два случая: 1) имеются данные многолетних наблюдений; 2) данных наблюдений мало или вообще нет.
При наличии многолетних наблюдений норма стока рассчитывается как среднеарифметическое из всех наблюденных величин по формулам (1), (12), (14)...(16). Этот расчет одинаково применим как для годового стока, так и для отдельных фаз водного режима. При этом надо иметь ввиду, что определять норму стока по формулам (1), (12), (14)...(16) можно обязательно при соблюдении следующих условий.
1. Рассматриваемы период наблюдений репрезентативен (представителен);
2. Ряд гидрометеорологических наблюдений однороден;
3. Относительная среднеквадратическая ошибка определения нормы
стока (4) не превышает 10%.
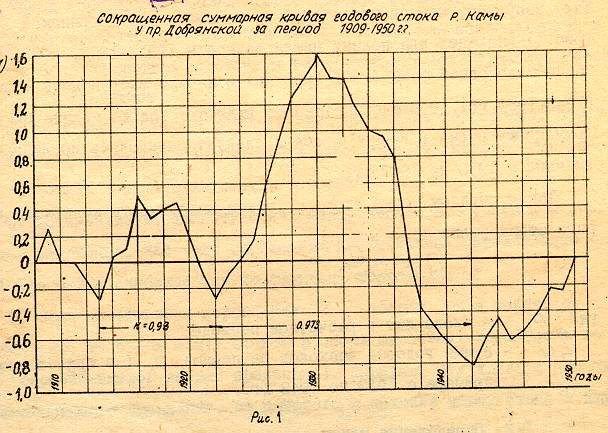
Репрезентативность периода наблюдений. Её оценивают с помощью сокращенной суммарной кривой стока, которую строят по зависимости
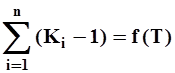
| (24) |
Сокращенная суммарная кривая имеет следующее свойство: тангенс угла наклона касательной, проведенной к кривой, характеризует отклонение рассматриваемой характеристики стока (в данном случае модульного коэффициента Кi ) от его среднего значения 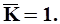
Используя это свойство сокращенной кривой, можно установить, что в период, в течение которого интегральная кривая имеет положительные тангенсы углов наклона (кривая поднимается вверх), т.е., когда Кi > 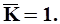 ,соответствует многоводной фазе колебаний стока. А период, когда тангенс углов, наклона отрицательный и Кi <
,соответствует многоводной фазе колебаний стока. А период, когда тангенс углов, наклона отрицательный и Кi < 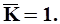 , относится к маловодной фазе. Экстремальные точки суммарной кривой позволяют определить начало и конец соответствующих фаз. (рис.1). Следовательно устанавливаются продолжительность полного цикла колебаний стока, включающего как многоводную, так и маловодную фазу речного стока (рис. 1). Как видно из этого рисунка, число лет наблюдений, которые необходимо для получения нормы стока с заданной точностью равно 30 лет.
, относится к маловодной фазе. Экстремальные точки суммарной кривой позволяют определить начало и конец соответствующих фаз. (рис.1). Следовательно устанавливаются продолжительность полного цикла колебаний стока, включающего как многоводную, так и маловодную фазу речного стока (рис. 1). Как видно из этого рисунка, число лет наблюдений, которые необходимо для получения нормы стока с заданной точностью равно 30 лет.
Оценка однородности ряда гидрометеорологических наблюдений. При определении нормы годового стока необходимо, чтобы наблюдения, образующие гидрологический ряд, были однородными, т.е. состояли из фазово-однородных величин, имеющих одинаковое происхождение.
Можно использовать два подхода.
Первый подход применяется тогда, когда имеется достаточно информации об изменении условий формирования стока на водосборе. В этом случае оценку однородности рядов наблюдений осуществляется на основе генетического (физического) анализа условий формирования речного стока с учетом влияния хозяйственной деятельности человека.
В тех же случаях, когда информации об изменении условий формирования стока на водосборе недостаточно, используются статистические методы оценки рядов наблюдений по однородности (второй подход).
Оценка осуществляется по численным значениям и среднеарифметической (Q0) и дисперсии (s2). При этом два ряда наблюдений признаются однородными, если однородны их средние значения и дисперсии. 
Для оценки однородности средних значений используют - t- критерий Стьюдента, а для оценки однородности дисперсий -F - критерий Фишера.
Сначала, используя формулы,
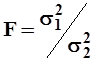 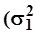 > > 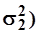 , ,
| (25) |
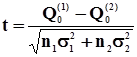 * * 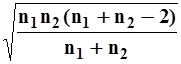
| (26) |
где 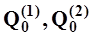 - выборочные среднеарифметические значения, по данным наблюдений соответственно за
- выборочные среднеарифметические значения, по данным наблюдений соответственно за 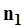 и
и 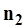 лет,
лет,
вычисляют статистики Fи t.
Затем при уровнях значимости a = 0.05 (или a = 0.01) и числа степеней свободы
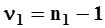 и и 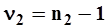
| (27) |
Определяют по таблице, приведенной в работе (Практикум по гидрологии, гидрометрии и регулированию стока. -М: Агропромиздат, 1988) табличные значения статистики 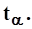
Если оказывается. что 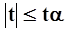 , то гипотеза однородности среднеарифметических значений сравниваемых рядов наблюдений принимается.
, то гипотеза однородности среднеарифметических значений сравниваемых рядов наблюдений принимается.
Аналогичным образом, если статистика F при данном уровне значимости a = 0.05 и числастепеней свободыn = n - 2оказывается меньше табличных значенийFa , т.е., еслиF<Fa,то Fпопадает в область допустимых значений и, следовательно, гипотеза об однородности дисперсий двух рядов принимается.
| <== предыдущая лекция | | | следующая лекция ==> |
| Определение расхода воды объемным методом. | | | гидрометрических данных. |
Дата добавления: 2015-05-21; просмотров: 3485;
