гидрометрических данных.
Определение нормы стока при недостаточном количестве
При недостаточном количестве гидрометрических данных, не обеспечивающих требуемой точности (5-10%), норму годового стока можно определить: методом корреляции; по графику связи годового стока в изучаемом бассейне и бассейне - аналоге с многолетними данными по стоку; по приближенной формуле. Сущность этих способов состоит в приведении коротких рядов наблюдений к длительным путям установления связи между годовым стоком в изучаемом бассейне (с коротким рядом наблюдений) и стоком в бассейне - аналоге с многолетними наблюдениями. Основное условие приведения стока к многолетнему периоду - наличие синхронности колебаний стока в изучаемом и аналогичном бассейнах. Кроме того, бассейн - аналог должен быть сходным с изучаемым по климатическим условиям, однотипности рельефа, почвогрунтов, гидрогеологических условий, залесенности, заболоченности и т.д.; площади водосборов не должны отличаться более чем в пять раз.
Определение нормы стока методом корреляции.
Сущность метода состоит в следующем:
а) Выбирают бассейн - аналог, имеющий данные по годовому стоку за многолетний период, включающий в себя годы, за которые имеются недостаточные данные в изучаемом бассейне.
б) Устанавливают тесноту связи между стоком в изучаемом и аналогичном бассейнах, для чего определяют по имеющимся параллельным в обоих бассейнах наблюдениям коэффициент корреляции r.
в) Если коэффициент корреляции r больше 0,8 и найден он достоверно, то связь между стоком в обоих бассейнах достаточно тесная (бассейн - аналог выбран правильно). Выражают эту связь с помощью корреляционного уравнения, из которого и находят норму стока в изучаемом бассейне.
В этой части расчетно-графической работы исходными данными являются среднегодовые модули стока (М) в изучаемом бассейне за период n=10 лет.
Используя данные параллельных наблюдений в изучаемом и аналогичном бассейнах (период n лет) вычисляем коэффициент корреляции по формуле
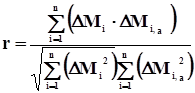
| (1) |
где 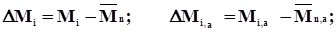
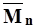 и
и 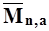 - средние значения годовых модулей стока в изучаемом и аналогичном бассейнах за короткий период времени (n=10 лет).
- средние значения годовых модулей стока в изучаемом и аналогичном бассейнах за короткий период времени (n=10 лет).
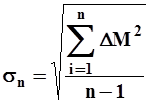
| (2) |
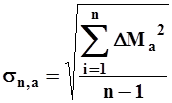
| (3) |
где 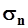 и
и 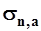 - средние квадратические отклонения годового стока подсчитанные по данным наблюдений за nлет.
- средние квадратические отклонения годового стока подсчитанные по данным наблюдений за nлет.
Вычисления, необходимые для расчета коэффициента корреляции по приведенным формулам ведем в табл. 2. В графу 2 таблицы выписываем годы параллельных наблюдений; в графы 3 и 4 - годовые модули стока за эти годы в изучаемом бассейне (М) и аналоге (Ма). Находим средние значения 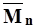 и
и 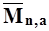 ,а затем отклонения в каждом году
,а затем отклонения в каждом году  и
и 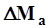 . Для контроля следует найти
. Для контроля следует найти 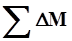 и
и 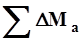 (суммы граф 5 и 6); эти суммы должны быть равны (или близки)нулю. Проверка всех вычислений в табл.2 производится по уравнениям:
(суммы граф 5 и 6); эти суммы должны быть равны (или близки)нулю. Проверка всех вычислений в табл.2 производится по уравнениям:
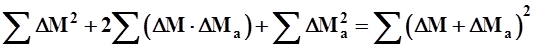
| (4) |
Расхождение допускаем не более 0,05.
По данным табл.2 вычисляем коэффициент корреляции по формуле (1), а также значения 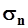 и
и 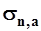 (2 и 3), необходимые в дальнейших расчетах.
(2 и 3), необходимые в дальнейших расчетах.
Так как коэффициент корреляции rопределен по небольшому ряду числу данных (всего за 10 лет), то необходимо проверить его достоверность. Оценку достоверности (неслучайности) коэффициента корреляции можно произвести с помощью коэффициента достоверности  ,равного отношению коэффициента корреляции к его среднему квадратическому отключению
,равного отношению коэффициента корреляции к его среднему квадратическому отключению
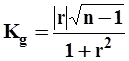
| (5) |
где 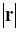 - абсолютная величина коэффициента корреляции; n- число членов ряда.
- абсолютная величина коэффициента корреляции; n- число членов ряда.
Значение коэффициента корреляции считается достоверным, если  >3.
>3.
По абсолютной величине rдолжен быть больше 0,8. Если эти условия выполняются (r>0,8 и  >3), то считаем, что связь между годовым стоком в рассматриваемых бассейнах достаточно тесная, бассейн - аналог выбран правильно.
>3), то считаем, что связь между годовым стоком в рассматриваемых бассейнах достаточно тесная, бассейн - аналог выбран правильно.
Таблица 2. К вычислению коэффициента корреляции между среднегодовыми модулями стока р. ... у ств. ... и р. ... у г. .....
| № п/п | Годы | Модули стока, л/с км2 | DM= | DMа= | DM2 | DMа2 | DM×DMа | DM+DMа | (DM+DMа)2 | ||||
| р. ... у ств. ... | р. ... у г. ... | M-Mn | M-Mn,a | ||||||||||
| . . | |||||||||||||
| Сумма | |||||||||||||
n=10 лет
Составляем корреляционное уравнение (уравнение регрессии) в виде
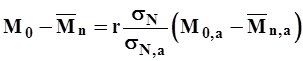
| (6) |
где 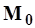 - норма стока в изучаемом бассейне;
- норма стока в изучаемом бассейне; 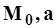 - норма стока в бассейне аналоге;
- норма стока в бассейне аналоге;
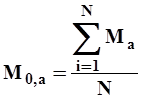
|
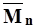 ,
, 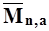 -средние значения годовых модулей стока в изучаемом бассейне и аналоге за короткий период времени n лет.
-средние значения годовых модулей стока в изучаемом бассейне и аналоге за короткий период времени n лет.
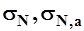 - средние квадратические отклонения годовых модулей стока в изучаемом и аналогичном бассейнах, подсчитанных по многолетнему ряду (N лет).
- средние квадратические отклонения годовых модулей стока в изучаемом и аналогичном бассейнах, подсчитанных по многолетнему ряду (N лет).
Среднее квадратическое отклонение 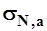 вычисляют по формуле
вычисляют по формуле
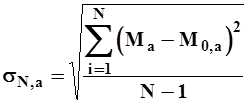
| (7) |
В изучаемом бассейне многолетние данные наблюдений отсутствуют, поэтому для определения среднего квадратического отклонения 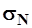 , используют формулу математической статистики вида
, используют формулу математической статистики вида
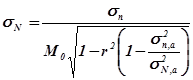
| (8) |
Из уравнения (6) искомая норма стока равна
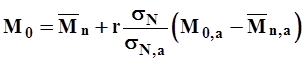
| (9) |
Для расчета величины 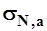 производим вычисления в таблице 3.
производим вычисления в таблице 3.
Таблица 3. Вычисление среднего квадратического отклонения годовых модулей стока р. ... у г. ..
за период ......-...... гг.
| №№ п.п. | Годы | Среднегодовые модули стока, Ма л/с.км2 | DМ=Ма-М0,а | (Ма-М0,а)2 |
| ... ... | ||||
| Сумма |
По формуле (7) находим sN,a .Среднеквадратическоеотклонение годового стока sN , приведенное к многолетнему периоду в изучаемом бассейне вычисляем по формуле (8). Далее, зная все члены правой части уравнения (9), определяем нормы стока в изучаемом бассейне. Относительная средняя квадратическая ошибка найденной нормы стока (М0) вычисляется по уравнению
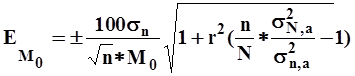
| 1(10) |
2.Определения нормы стока методом корреляции состоит в следующем. Выражаем связь между годовым стоком в изучаемом и аналоичном бассейнах корреляционным уравнением вида

| 1(11) |
где М и Ма - текущие координаты уравнения.
Пользуясь уравнением (11) удлиняем ряд наблюдений в изучаемом бассейне. Для этого в уравнение (11) подставляем последовательно модуль стока аналоге (Ма) и находим соответственно модуль стока в изучаемом бассейне (М) за все недостающие годы, т.е. получаем столько членов ряда, сколько имеется наблюдений в аналоге. Так, например для рассматриваемых бассейнов (изучаемым и аналогичным) 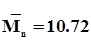 л/(с км2); r=0.98; sn =2.325(л/ с км2)
л/(с км2); r=0.98; sn =2.325(л/ с км2)
sn,а =2.173 л/( с км2); 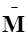 n,a=10,3 л/ (с км2) ;
n,a=10,3 л/ (с км2) ;
тогда
.
Допустим, что годовой модуль стока реки аналога в 1919 г.
Ма=10.0 л/ (с км2).Из уравнения (11) находим годовой модуль стока в изучаемом бассейне в 1919 г.
М1919= 10.72+0.98 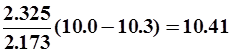 л/( с км2)
л/( с км2)
в 1920 г. Ма = 6.8л/( с км2), тогда
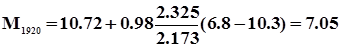 л/ (с км2)
л/ (с км2)
Аналогично определяем значение годового стока изучаемого бассейна для всех последующих лет за которые имеются наблюдения в аналоге.
По удлиненному ряду находим норму стока, как среднее арифметическое
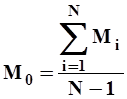
| 1(12) |
3. Определение нормы стока по графику связи.Исходные данные: годовые модули стока в изучаемом бассейне за период n=10 лет.
В данной работе бассейн-аналог указан и приведены данные наблюдений в нем за многолетний период (n=25 лет).
Данные одновременных наблюдений (за период n лет) наносятся на координатную сетку, откладывая по оси ординат годовые модули стока в изучаемом бассейне (М), по оси абсцисс - модули стока в бассейне- аналоге (Ма). По этим точкам проводим линию связи таким образом, чтобы она удовлетворяла равномерному расположению точек по обе стороны. Масштаб построения графика связи выбирают так, чтобы линия связи проходила примерно под углом 450 .Для построения удовлетворительной прямолинейной связи годовых значений стока необходимо иметь одновременные наблюдения в изучаемом и аналогичном бассейне не менее 6 лет (n ³ 6 лет). Отклонение большей части точек от линии связи не должно превышать 15%.
Вычислив норму стока в бассейне аналоге непосредственно по длинному ряду наблюдений ( 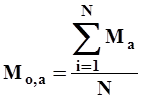 ), откладываем ее значения на оси абсцисс и по графику связи находим норму стока в изучаемом бассейне.
), откладываем ее значения на оси абсцисс и по графику связи находим норму стока в изучаемом бассейне.
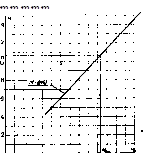
На рис. 1 приведен график связи между годовыми модулями стока р.Камы у пр. Дворянской и р. Камы у г. Перми за 1909 - 1918 гг. По норме стока аналога Мо,а=10.26 л/(с км2) графически определяем соответствующее ей значение нормы в расчетном створе (р.Кама у пр. Дворянская) Мо=10.7 л/(с.км2).
 Mn,a
Mn,a
Рис.1. График связи между годовыми модулями стока р. Камы у пр. Добрянская (М) и р. Камы у г. Пермь (М0).
3. Определение нормы стока по приближенной формуле.Норму стока по приближенной формуле определяют при очень коротком периоде наблюдений (n< 6 лет). Этот способ исходит из предположения, что линия связи стока в двух бассейнах проходит через начало координат и соотношение стока за различные периоды остается постоянным, а именно
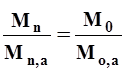
| (13) |
где Мn , Mn,a - среднее значение стока в изучаемом и аналогичном бассейне за одновременный короткий период наблюдений;
Мо, Мо,а - норма стока в изучаемом и аналогичном бассейне. Отсюда норма стока в изучаемом бассейне (с коротким периодом наблюдений) равна
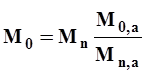
| (14) |
Формула (14) может быть использована в случае, когда отношение 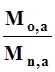 находится в пределах 0.8-1.4, а отношение коэффициентов вариации стока в изучаемом и аналогичном бассейне
находится в пределах 0.8-1.4, а отношение коэффициентов вариации стока в изучаемом и аналогичном бассейне 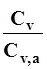 в пределах 0.8 - 1.2. Расчет по формуле (14) производим по тем же исходным данным, что и в предыдущем параграфе.
в пределах 0.8 - 1.2. Расчет по формуле (14) производим по тем же исходным данным, что и в предыдущем параграфе.
4. Определение нормы стока при отсутствии гидрометрических данных.При отсутствии наблюдений над стоком норму стока для какой-либо неизученной реки можно приближенно определить по картам изолиний среднего годового стока. Такая карта для всего Советского Союза составлена в 1946 г. Б.Д. Зайковым.
В 1962 г. опубликована уточненная карта К.П. Воскресенским по большому количеству пунктов наблюдений и по более длинным рядам стока.
Как это было показано на рис.2, для определения нормы стока какой-либо неизученной реки на карте изолиний стока проводится водораздельная линия бассейна реки до замыкающего створа А и определяется М - центр тяжести бассейна; значение модуля стока для центра тяжести М определяется путем интерполяциии между соседними изолиниями, в рассматриваемом примере - между изо-линиями 5 и 6 л/сек с 1 км2, и получается равным 5.3 л/(с км2). Это значение и принимается в качестве нормы стока для бассейна реки до замыкающего створа А.
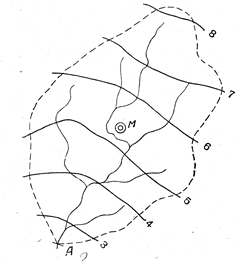
Рис.2. Определение среднего многолетнего стока по карте изолиний модулей стока (л/сек с 1 км2).
Определив норму стока в виде модуля, можно вычислить значение среднего годового многолетнего расхода по формуле
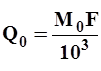 м3/сек, м3/сек,
| (15) |
где М0 - модуль стока, определенный по карте для центра тяжести бассейна, в л /сек с км2 ; F - площадь бассейна до данного замыкающего створа в км2.
Для очень больших речных водосборов и при различии в нормах стока на отдельных составляющих водосбора следует определять по карте изолиний средневзвешенный модуль стока по следующей формуле
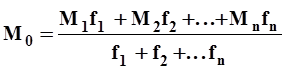 л /сек с км2 л /сек с км2
| (16) |
где М1, М2, ..., Мn - средние арифметические значения модулей стока соседних изолиний, ограничивающих отдельные бассейна, f1, f2,..., fn - площади бассена между соседними изолиниями стока, определяемые планиметрированием.
Определение нормы стока по картам изолиний на Европейской территории России для больших бассейнов может быть сделано с точностью до 3-5 % ; для малых бассейнов точность определения нормы стока рек значительно снижается.
Распределение нормы стока рек по территории РФ имеет ясно выраженную широтную зональность.
В заключении первой части настоящей расчетно-графической работы следует произвести сопоставление результатов расчета нормы годового стока различными способами, принимая в качестве основного способа - определение нормы стока по многолетним гидрометрическим данным.
Для рассмотренного примера результаты расчета нормы годового стока приведены в таблице 4.
Таблица 4
| Много-летний ряд | Метод корреляции --------------------------- | График связи | Приближенная формула | Карта изолиний | ||
| Уравнение регоессии | Удлиненныйряд | |||||
| М л/с.км2 | ||||||
| % отклоне-ния | - |
| <== предыдущая лекция | | | следующая лекция ==> |
| Обоснование применения методов математической статистики в гидрологии. | | | Изменчивость характеристики стока. |
Дата добавления: 2015-05-21; просмотров: 1431;
