Трехкомпонентные системы.
На практике наряду с двухкомпонентными системами гораздо чаще приходится иметь дело с системами, составленными из трех и более компонентов.
Уравнение состояния трехкомпонентных систем связывает между собой пять параметров и имеет следующий вид:
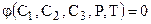 . (6.12)
. (6.12)
Из (6.12) следует, что диаграмма состояния трехкомпонентной системы не может быть изображена на плоскости.
Полагая, что Р = const и С1 + С2 + С3 = 1, если способ выражения состава сплавов мольные доли, трехкомпонентную диаграмму можно построить в трехмерном пространстве.
Составы трехкомпонентных сплавов принято изображать на плоскости с помощью концентрационного треугольника. В вершинах треугольника располагаются чистые компоненты А, В и С, а три его стороны отражают составы двойных сплавов. Ось, перпендикулярная плоскости концентрационнго треугольника - температурная ось.
Свойства концентрационного треугольника.
Первое свойство. Если из какой-то точки М, лежащей в плоскости треугольника опустить три перпендикуляра на стороны, то:
МА + МВ + МС = const = BD,
где BD - высота концентрационного треугольника (рис. 6.9, а).
Если BD принять за 100%, то каждый из перпендикуляров - концентрация каждого из компонентов в сплаве:
Ма = % А; Мb = % B; Mc = % C.
Второе свойство. Если через точку М, лежащей в плоскости треугольника, провести три
параллельные сторонам треугольника прямые, то сумма отрезков Аb, Bc и Са, отсекаемых этими прямыми на сторонах треугольника - величина постоянная и равная стороне треугольника:
Аb + Вс + Са = const = АВ.
Если АВ = % В, Вс = % С и Са = % А, то состав трехкомпонентного сплава определен.
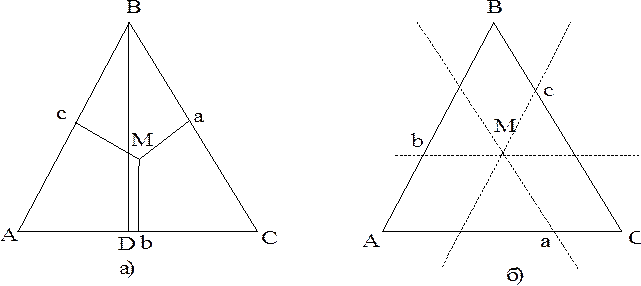
|
| Рис. 6.9. Свойства равностороннего треугольника, применяемого для изображения составов трехкомпонентных сплавов. |
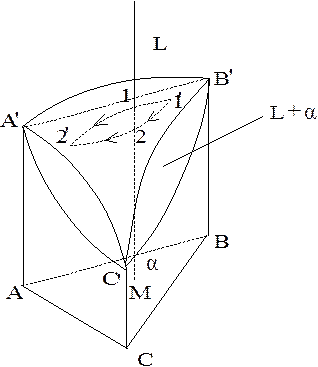
|
Таким образом, зная свойства равностороннего треугольника, по положению фигуративной точки можно оценить состав трехкомпонентного сплава или, зная его состав, можно найти положение фигуративной точки в плоскости концентрационного треугольника.
Как и для двухкомпонентных систем, сложность диаграмм состояния трехкомпонентных систем зависит от взаимной растворимости компонентов и от возможности образования между ними химических соединений.
Наиболее простой является диаграмма состояния трехкомпонентной системы с неограниченной растворимостью компонентов в жидком и твердом состояниях (рис. 6.10).
Для диаграммы на рис. 6.10 ТS (B) > ТS (A) > ТS (С) т. А’, B’ и C’ - температуры плавления чистых компонентов.
| Рис. 6.10. Диаграмма состояния тройной системы с неограниченной растворимостью компонентов в жидком и твердом состояниях. |
Грани призмы - двойные системы с неограниченной растворимостью компонентов в твердом и жидком состояниях. Через три ликвидуса проходит поверхность ликвидуса. Выше поверхности ликвидуса находится объем жидких растворов (L). Через три солидуса проходит поверхность солидуса. Ниже поверхности солидуса располагается объем твердых растворов ( 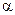 ). Объем пространства между поверхностями ликвидуса и солидуса занят равновесной двухфазной системой из жидких и твердых растворов (L +
). Объем пространства между поверхностями ликвидуса и солидуса занят равновесной двухфазной системой из жидких и твердых растворов (L + 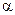 ). Интервал между поверхностью ликвидуса и солидуса - интервал кристаллизации (плавления) сплавов трехкомпонентной системы.
). Интервал между поверхностью ликвидуса и солидуса - интервал кристаллизации (плавления) сплавов трехкомпонентной системы.
Сплав состава т. М (рис. 6.10) при Т > Т1 находится в состоянии ненасыщенного жидкого раствора. Кристаллизация сплава начинается при Т1, лежащей на поверхности ликвидуса. Состав первых кристаллов 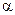 - твердого раствора соответствует проекции точки 1’ на плоскость концентрационного треугольника.
- твердого раствора соответствует проекции точки 1’ на плоскость концентрационного треугольника.
При дальнейшем понижении температуры от Т1 до Т2 жидкость постепенно принимает состав т. 2’ и исчезает, а кристаллы 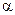 - твердого раствора - т. 2. Поэтому процесс кристаллизации сплава изображается уравнением вида:
- твердого раствора - т. 2. Поэтому процесс кристаллизации сплава изображается уравнением вида:
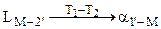 . (6.10)
. (6.10)
Ниже температуры Т2 происходит охлаждение кристаллов твердого раствора 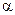 .
.
При работе с диаграммами состояния трехкомпонентных систем удобно пользоваться их разрезами - поли- и изотермическими. Изотермические разрезы характеризуют фазовые равновесия в тройных сплавах, а по политермическим разрезам устанавливают температуры начала и конца кристаллизации сплавов и т.д.
_______
В данной главе рассмотрен ряд более или менее сложных систем, изучение которых с помощью лишь одного термодинамического метода затруднено. С помощью же диаграмм состояния свойства таких систем описывать достаточно просто. Но лишь параллельное применение термодинамического метода и основных позиций физико-химического анализа, с помощью которого строятся диаграммы состояния, позволяет получить весьма глубокую информацию об изучаемой системе. Однако всегда необходимо помнить, что большей частью рассматриваются лишь равновесные системы. Именно для таких систем изображаются соответствующие диаграммы состояния. Количество и конкретный вид фаз сложной системы, наблюдаемые на практике, могут в действительности сильно отличаться от равновесных, вследствие торможения процесса перехода в равновесное состояние.
Дата добавления: 2015-05-21; просмотров: 3270;
