Определение степени деформации при резании
Представим зону деформации ограниченной двумя прямыми параллельными линиями [2] (рис. 4.4).
Ширина зоны деформации равна ∆y, т.е. стороне элементарного квадрата. Вершина квадрата (точка А) находится на пересечении обрабатываемой поверхности с верхней границей зоны деформации. После деформации квадрата точка А перемещается на свободную поверхность стружки в точку А'. Расстояние между точками А и А' равно абсолютному сдвигу ∆x. Запишем выражение для относительного сдвига (см. 4.6):
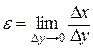
Выразим ∆x и ∆y через скорость сдвига V2 и скорость Vy, перпендикулярную плоскости сдвига. Для этого разделим числитель и знаменатель выражения (6.6) на ∆t – время, в течение которого частица металла проходит через зону деформации.
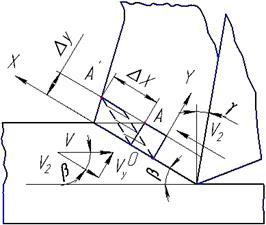
Рис. 4.4. Схема простого сдвига при резании:β – угол наклона плоскости сдвига
Получим
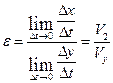 . (4.9)
. (4.9)
Из рисунка 4.4 имеем:
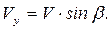 (4.10)
(4.10)
Подставив (4.5) и (4.10) в выражение (4.9), получим
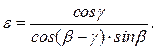 (4.11)
(4.11)
Кроме формулы (4.11) для расчета относительного сдвига могут быть использованы другие формулы, тождественные (4.11):
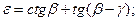 (4.12)
(4.12)
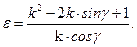 (4.13)
(4.13)
Дата добавления: 2015-05-21; просмотров: 932;
