П.3. Уравнение турбулентной диффузии в рамках модели Лайхтмана Д.Л.

Рассматривая в качестве субстанции объемную активность радиоактивной примеси, при определенных метеопараметрах u(z), v(z) и k(z) перенос последней в атмосфере рассчитывают, используя уравнение турбулентной диффузии. При этом формулируют задачу следующим образом. Предполагают, что размывание примеси по оси Y осуществляется по закону Гаусса, определяя, таким образом объемную активность примеси выражением:

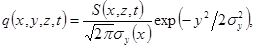(П.14.2)

где 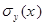- среднеквадратичное отклонение. Интегрируя уравнение (13.6) гл. 13 в соответствии с выражением:

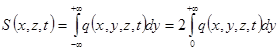, (П.14.3)

и, используя (П.14.2), получают:

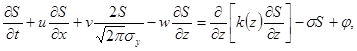(П.14.4)

где 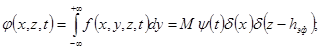f = My(t)d(x)d(y)d(z-h_эф) – источник радиоактивной примеси; M – мощность выброса Бк/с; h_эф – эффективная высота выброса; y(t)–изменение при выбросе объемной активности радиоактивной примеси во времени. В качестве постоянной релаксации радиоактивной примеси s будем рассматривать величину, представляющую собой сумму постоянной вымывания примеси из атмосферы s₀ и постоянной ее радиоактивного распада l, так что s = s₀ + l. 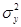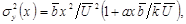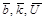В рамках рассматриваемой модели переноса величину (x) представляют в виде: где - усредненные по пограничному слою с весом q(x, z, t) значения энергии турбулентных пульсаций b(z), коэффициента турбулентной диффузии k(z) и скорости ветра 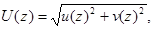a – постоянная.

.

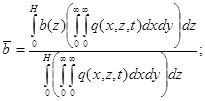
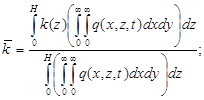
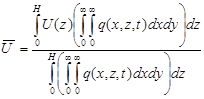(П.14.5)

Обрабатывая граничные и начальные условия аналогично выражению (П.14.3), получают:

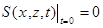; (П.14.6)

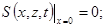(П.14.7)

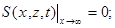
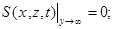(П.14.8)

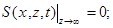
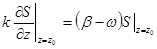. (П.14.9)

Для стационарного уравнения первый член в формуле (П.14.4) будет равен нулю, в формулах (П.14.5) ¾ (П.14.9) исчезает переменная t, величина M будет постоянной, а уравнение при этом приобретает вид:

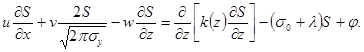(П.14.10)