П.2. Принципы размещения постов контроля АСКРО

 Из имеющихся методов решения систем уравнений подобных (13.4) П.13.2, гл.13 наибольшее применение получили методы регуляризации и итеративной регуляризации, в которых искомое решение находят, учитывая погрешность как правой части уравнения (13.4), так и оператора
Из имеющихся методов решения систем уравнений подобных (13.4) П.13.2, гл.13 наибольшее применение получили методы регуляризации и итеративной регуляризации, в которых искомое решение находят, учитывая погрешность как правой части уравнения (13.4), так и оператора 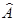 , если она есть (в данной задаче эта погрешность может быть обусловлена фактором накопления). Вместе с тем, для задач спектрометрии ионизирующего излучения разработаны и специальные методы, особенностью которых является жесткое требование положительности решения jj ³ 0, j = 1,2,3,..,M и отсутствие погрешности в операторе
, если она есть (в данной задаче эта погрешность может быть обусловлена фактором накопления). Вместе с тем, для задач спектрометрии ионизирующего излучения разработаны и специальные методы, особенностью которых является жесткое требование положительности решения jj ³ 0, j = 1,2,3,..,M и отсутствие погрешности в операторе 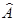 . Для проверки методов расчета jj использует так называемый метод “бумажного эксперимента”: задают исходный спектр jапр(E), затем по уравнению (13.4) находят значения D(Ri), которые искажают в пределах погрешности реальных показаний датчиков (15¾25 %), после чего решают обратную задачу определения jj. Из представленных на рис. П.14.3 результатов решения уравнения (13.4) следует, что исходный и восстановленный спектры удовлетворительно согласуются, а в табл. П.14.1 вместе с указанными спектрами приведено решение системы линейных алгебраических уравнений, полученное тривиальным обращением матрицы (неудовлетворительное решение):
. Для проверки методов расчета jj использует так называемый метод “бумажного эксперимента”: задают исходный спектр jапр(E), затем по уравнению (13.4) находят значения D(Ri), которые искажают в пределах погрешности реальных показаний датчиков (15¾25 %), после чего решают обратную задачу определения jj. Из представленных на рис. П.14.3 результатов решения уравнения (13.4) следует, что исходный и восстановленный спектры удовлетворительно согласуются, а в табл. П.14.1 вместе с указанными спектрами приведено решение системы линейных алгебраических уравнений, полученное тривиальным обращением матрицы (неудовлетворительное решение):
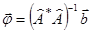 ,
,
где 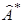 - матрица сопряженная
- матрица сопряженная 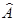 , а
, а 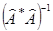 - обратная матрица размером M‰M;
- обратная матрица размером M‰M; 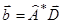 - вектор.
- вектор.
При решении некорректных задач обычно рассматриваются два случая. В первом задается погрешность в правой части (векторе D) и во втором - погрешность задается в правой части и ядре уравнения (13.3). Мы при решении данной задачи ограничимся первым случаем. Вместе с тем, для того и другого случаев разработан устойчивый метод решения задачи. Однако, для рассматриваемой задачи могут быть использованы и другие методы: метод (Y. Su, N. Scoffield, H. Fabian). Эти методы отличаются от метода А.Н. Тихонова тем, что они требуют строгой положительности решения, что полностью отвечает рассматриваемой задаче. Между собой эти методы отличаются определенным алгоритмом, суть которого сводится к поправке диагональных элементов матрицы. Последнее определяет скорость сходимости задач, которые решают, используя итерационные процедуры. Из рис.П.14.3 следует, что значение средней энергии восстановленных спектров меньше исходного. Последнее нетрудно понять, если учесть, что средняя энергия представленных распределений также представляет собой интегральную величину:
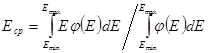 . (П.14.1)
. (П.14.1)
Поэтому наличие погрешности в спектральных распределениях, возникающих при задании погрешности измерения датчиков, подтверждает справедливость формулы, описывающей оценку средней величины аргумента случайной функции при заданной её относительной погрешности δ, которая для средней энергии <Etot>
будет иметь вид: <Etot> = <Eср>(1 – δ).
| Таблица П.14.1 Сравнение исходного jапр и восстановленных спектров | |||||
| Индекс, j | Энергия Ej , МэВ | Cпeктр φ(Ej) | |||
| Априорный | Вычисленный методом | ||||
| Su Y. | Тихонова А.Н. | обр. матр. | |||
| 0,37 | 1,768 | 1,784 | 1,851 | -0,088 | |
| 0,748 | 0,503 | 0,731 | 0,671 | 0,0 | |
| 1,1216 | 0,328 | 0,149 | 0,137 | -0,802 | |
| 1,496 | 7,36E-2 | 1,56E-2 | 1,45E-2 | -1,1E-3 | |
| 1,87 | 9,6 E-4 | 2,28E-4 | 2,13E-4 | 2,8434 |
Условие Ri ¹ Ri+1 ¹ Ri+2..¹ 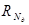 , i = 1,2,3..Nд накладывает определенные требования на размещение g-датчиков АСКРО, которые сводятся к исключению осевой и центральной симметрии при их размещении, поскольку в противном случае число уравнений вида (13.3) или (13.4), отличающихся правой частью, уменьшится в 2 или 4 раза (при осевой симметрии) или приведет к полному вырождению системы линейных алгебраических уравнений (при размещении датчиков по периметру санитарно-защитной зоны, т.е. при центральной симметрии). Кроме того, как уже отмечалось, размещение датчиков по периметру зоны надежно регистрирует факел выброса или распространение облака при любом направлении ветра. Учет этих двух противоречивых требований приводит к тому, что Ri g-датчиков должно возрастать с увеличением азимутального угла, отсчитываемого от какого-либо направления (например, как в спирали Архимеда). Графики таких кривых приведены на рис. 13.2, П.13.2 гл.13 и представляют собой либо гладкую кривую, для которой Ri, является функцией угла, Ri = R0qi,qi = iDq; I = 1,2,.,Nд; Dq = 2p/Nд, либо многолучевую звезду. При этом каждый из датчиков Ni, где i = 1,2,...,Nд установлен на расстоянии радиуса Ri от источника радиоактивных выбросов (на расстоянии ri, от основания источника), отличном от соответствующих рассиряний всех остальных γ-датчиков на величину DRi (Dri на подстилающей поверхности).
, i = 1,2,3..Nд накладывает определенные требования на размещение g-датчиков АСКРО, которые сводятся к исключению осевой и центральной симметрии при их размещении, поскольку в противном случае число уравнений вида (13.3) или (13.4), отличающихся правой частью, уменьшится в 2 или 4 раза (при осевой симметрии) или приведет к полному вырождению системы линейных алгебраических уравнений (при размещении датчиков по периметру санитарно-защитной зоны, т.е. при центральной симметрии). Кроме того, как уже отмечалось, размещение датчиков по периметру зоны надежно регистрирует факел выброса или распространение облака при любом направлении ветра. Учет этих двух противоречивых требований приводит к тому, что Ri g-датчиков должно возрастать с увеличением азимутального угла, отсчитываемого от какого-либо направления (например, как в спирали Архимеда). Графики таких кривых приведены на рис. 13.2, П.13.2 гл.13 и представляют собой либо гладкую кривую, для которой Ri, является функцией угла, Ri = R0qi,qi = iDq; I = 1,2,.,Nд; Dq = 2p/Nд, либо многолучевую звезду. При этом каждый из датчиков Ni, где i = 1,2,...,Nд установлен на расстоянии радиуса Ri от источника радиоактивных выбросов (на расстоянии ri, от основания источника), отличном от соответствующих рассиряний всех остальных γ-датчиков на величину DRi (Dri на подстилающей поверхности).
Таким образом, предложенный метод расстановки g-датчиков АСКРО, представленный на рис. 13.2, с учетом их необходимого и достаточного количества и равномерности азимутального их распределения вокруг АЭС, учитывает экономические, экологические и физические принципы, которые дают основания говорить, что метод, действительно является оптимальным.
Дата добавления: 2015-05-19; просмотров: 872;
