Схемная реализация комбинационных схем на логических элементах
Логическими элементами называются микросхемы малой степени интеграции, реализующие простейшие логические функции двух — четырех аргументов. Наиболее распространены логические элементы, реализующие логические функции И (рис. 5.5,а), ИДИ (рис. 5.5,б), И-НЕ (рис. 5.5,в) и ИЛИ-НЕ (рис. 5.5,г). К логическим элементам относятся также микросхемы, реализующие простейшие последовательностные алгоритмы (например, триггеры), но они будут рассмотрены далее.
Логические элементы И реализуют функцию логического умножения (конъюнкцию). Это означает, что выходной сигнал схемы И равен единице только в том случае, когда все ее входные сигналы равны единице. Логический элемент И называется также схемой совпадения.
Логические элементы ИЛИ реализуют функцию логического сложения (дизъюнкцию), т.е. сигнал на выходе схемы ИЛИ равен нулю только тогда, когда все входные сигналы равны нулю.
Логические элементы И —НЕ реализуют функцию инверсии логического произведения (функцию Шеффера), а элементы
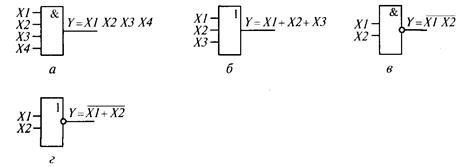
Рис. 5.5. Схемные обозначения логических элементов И (а), ИЛИ (б), И-НЕ (в), ИЛИ-НЕ (г)
ИЛИ —НЕ — функцию инверсии логической суммы (функцию Пирса). Таким образом, если логическое произведение равно единице, то элемент И —НЕ выдает нулевой сигнал на своем выходе; если логическая сумма равна единице, то элемент ИЛИ —НЕ также выдает нулевой сигнал. В противном случае на выходах элементов данного типа формируется единичный сигнал (см. табл.. П4.1 Приложения 4).
В одном корпусе микросхемы обычно имеется четыре логических схемы — на два входа каждая, либо три схемы — на три входа каждая, либо две схемы — на четыре входа каждая независимо от вида элементарных логических функций, которые данные микросхемы реализуют. Если не все входы логической схемы используются в проектируемом устройстве, то неиспользуемые входы следует объединять с используемыми. Так, для реализации функции инверсии необходимо объединить все входы схемы И — НЕ (рис. 5.6, а). Тогда получим
Y = ~XX = X.
Если две схемы И —НЕ соединить последовательно, как показано на рис. 5.6, б, то вторая схема инвертирует инверсию логического произведения, полученного на первой схеме, так что на выходе второй схемы получим само логическое произведение.
Если же на вход схемы И — НЕ подать инверсии интересующих нас сигналов (рис. 5.6, в), полученных предварительно с помощью схемы И —НЕ, то на выходе получим логическую сумму исходных сигналов согласно закону Де Моргана (см. подразд. П4.3 Приложения 4). Таким образом, с помощью элементов И —НЕ можно реализовать все базовые функции булевой алгебры, а следовательно, любые логические функции. Так же универсальны и элементы ИЛИ —НЕ. Элементы других типов, которые при наличии элементов И —НЕ или ИЛИ —НЕ не являются обязательными для реализации алгоритмов управления, имеют, как правило, специальное назначение. Так, элементы И (см. рис. 5.5, а) обычно являются усилительными элементами. Их допустимый выходной ток достигает 100 мА, в то время как обычные логические элементы имеют допустимый выходной ток до 5 мА.

Рис. 5.6. Реализация базовых логических функций на элементах И —НЕ: а — инверсия; б — логическое произведение; в — логическая сумма.
ЗАДАЧИ МИНИМИЗАЦИИ ФУНКЦИЙ
Принимая во внимание проблемы оптимизации проектируемого устройства, можно утверждать, что в общем случае схема с меньшим количеством элементов обходится дешевле и более надежна в работе, а из двух схем с одинаковым количеством логических элементов лучше та, которая оперирует меньшим числом сигналов (имеет меньшее суммарное число входов всех элементов). Итак, независимо от применяемых в дальнейшем при построении логической схемы элементов очень важным этапом синтеза является поиск такого вида логической функции, в котором имеется минимальное число букв (переменных и их отрицаний)1. Процесс поиска такого вида называется минимизацией функции и основывается на так называемых правилах склеивания:
Ax\jAx=A; (Ву х)(Ву х)=В,
в которых А и В - переменные или логические функции. Эти правила можно сформулировать следующим образом: дизъюнкция или конъюнкция двух выражений, отличающихся одно от другого только знаком отрицания для одной переменной, могут быть заменены одним выражением без той переменной, по которой они отличаются. Например:
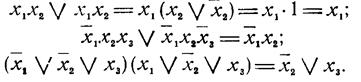
Выражения, для которых возможно склеивание, называются соседними выражениями. Если в полученных канонических представлениях имеются соседние выражения, то соответствующие представления можно упростить с целью получения простой технической реализации.
МЕТОД МАТРИЦ КАРНО
Метод матриц Карно (диаграмм Вейча) облегчает процедуру склеивания благодаря тому, что члены СДНФ или СКНФ (полные конъюнкции или полные дизъюнкции) размещаются на плоскости таким образом, что соседние члены, для которых возможно склеивание, оказываются в непосредственной близости друг от друга.
Примеры матриц Карно приведены на рис. 3-2. Каждая клетка матрицы соответствует одной комбинации значений входных переменных. Код этих комбинаций подобран так, чтобы соседние клетки отличались значениями только одной переменной, т. е. чтобы им соответствовали соседние выражения (код Грея). В построенную на основе этого кода таблицу вписываются символы, соответствующие значениям функции на определенных наборах входных переменных. Процедура облегчается, если функция задана десятичными индексами входных наборов. Такие матрицы, заполненные десятичными числами, представлены на рис. 3-2.
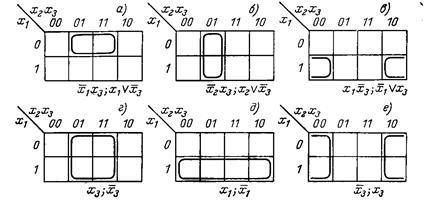
Рис. 3-3.. Примеры объединения ирезультаты склеивания в матрицах для трех переменных.
Если в двух соседних клетках заполненной матрицы Карно находятся одинаковые символы (0 или 1), то соответствующие этим клеткам выражения можно склеить, что равносильно устранению переменной, которая в рамках склеиваемой группы меняет значение. Соседние клетки матрицы, образующие пары, объединяются замкнутой линией для обозначения возможности склеивания.
Итак, одинаковые символы, охваченные контуром, можно представить конъюнкцией (если эти символы суть единицы) или дизъюнкцией (если эти символы нули), в которые входят только переменные, не меняющиеся в пределах этого контура. На рис. 3-3 под соответствующими матрицами приведены результаты склеивания, причем на первом месте даны выражения, представляющие группу единиц, а через точку с запятой — выражения, представляющие группу нулей.
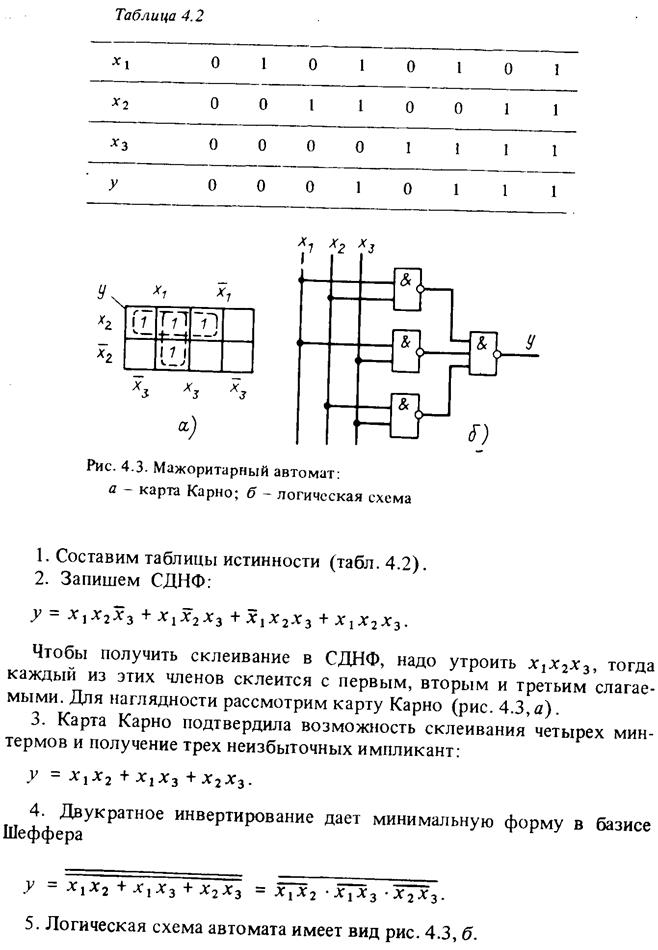
Пример 4.2. Разработать автомат, реагирующий не менее чем на два сигнала из трех (мажоритарный автомат).
Дата добавления: 2015-05-16; просмотров: 1912;
