Параллакстық үшбұрыш және аспан координаттарын өзара түрлендіру

Параллакстық үшбұрыш деп аспан сферасындағы шырақтың вертикал сызығы, сағаттық шеңбері және аспан меридианы доғаларынан құралған үшбұрышты атаймыз (1.11 сурет). Оның төбелері әлем полюсі P, зенит Z және шырақ M болып табылады. Енді осы үшбұрыштың қабырғалары мен бұрыштарын табайық. Егер шырақ аспан сферасының батыс бөлігінде орналасқан болса (1.11 суреттің сол жағы), ZP қабырғасы 90º-j тең (j - бақылау орны ендігі), ZM қабырғасы шырақтың зениттік қашықтығына тең z=90º-h (h - шырақ биіктігі), PM қабырғасы шырақтың полюстік қашықтығына тең p=90º-d (d - шырақ ауысуы). Z төбесіндегі бұрышы 180º-А тең (А - шырақ азимуты), Р төбесінің бұрышы t сағаттық бұрышқа тең, ал М төбесіндегі бұрышы q - параллакстық бұрыш деп аталады. Егер шырақ аспан сферасының шығыс бөлігінде орналасқан болса (1.11 суреттің оң жағы), Р төбесіндегі бұрышы 360º-t тең, Z төбесіндегі бұрышы А-180º тең болады, ал қабырғалары сол күйі қалады.

Тікелей өлшеулер арқылы z (немесе h) пен А анықталады, j - бақылау орны ендігі белгілі десек, шырақтың ауысуын d, сағаттық бұрышын t және тік шарықтауын a=s-t (s-жұлдыздық уақыт) сфералық үшбұрыштарға арналған формулалардан шығарылған мына қатынастар арқылы таба аламыз:

sin d = sin j cos z – cos j sin z cos A,

cos d sin t = sin z sin A, (1.6.1)

cos d cos t = cos j cos z + sin j sin z cos A,

яғни бұл қатынастар горизонталды координаттар жүйесінен экваторлық координаттар жүйесіне өту үшін қолданылады.

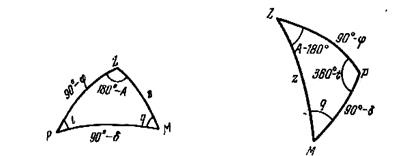
1.16 сурет – Параллакстық үшбұрыш

Егер d, t және j белгілі болып, z және А-ны табу керек болса, онда мына қатынастарды қолданамыз

cos z = sin j sin d + cos j cos d cos t,

sin z sin A = cos d sin t, (1.6.2)

sin z cos A = - cos j sin d + sin j cos d cos t,

яғни бұл қатынастар экваторлық координаттар жүйесінен горизонталды координаттар жүйесіне өту үшін қолданылады. Сонымен қоса жоғарыдағы формулалар шырақтардың шығу және бату уақыттары мен азимуттарын есептеу үшін, бақылау орнының географиялық ендігін және жергілікті жұлдыздық уақытты анықтау үшін қолданылады.