Теоретическая часть. Рассмотрим подробнее, как проводится теоретический анализ треков заряженных частиц, движущихся со скоростями
Рассмотрим подробнее, как проводится теоретический анализ треков заряженных частиц, движущихся со скоростями, близкими к скорости света. Для этого необходимо рассмотреть основные положения динамики больших скоростей.
В 1905 г. Альберт Эйнштейн объяснил многие экспериментальные результаты, не укладывающиеся в рамки классической физики, в своей теории относительности. В основу первой части теории, названной специальной теорией относительности (СТО), Эйнштейн положил два постулата:
1. Никакими опытами внутри любой равномерно движущейся системы нельзя обнаружить, движется ли эта система или находится в состоянии покоя. Иначе говоря, нельзя обнаружить абсолютное движение тел.
2. Скорость света в вакууме, равная 3·108 м/с, является постоянной величиной (не зависит от относительной скорости источника и наблюдателя).
Существует три взаимосвязанных аспекта СТО:
- электродинамика движущихся тел;
- теория пространства и времени;
- механика быстрых движений.
Нас будет интересовать третий аспект. Рассмотрим, как преобразуются выражения для импульса, скорости и кинетической энергии в случае больших скоростей.
В нерелятивистском случае (v<<с) второй закон Ньютона и закон сохранения механической энергии имеют вид:
 ; (8.1)
; (8.1)
 . (8.2)
. (8.2)
Импульс 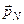 и энергия ЕN определяются соответственно как
и энергия ЕN определяются соответственно как  и
и  (сумма кинетической
(сумма кинетической 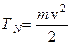 и потенциальной U энергии тела). Если работа сторонних сил над телом
и потенциальной U энергии тела). Если работа сторонних сил над телом 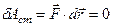 , то
, то  , а значит
, а значит 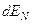 =const.
=const.
При  и
и  (
(  - импульс тела в начальный момент времени)
- импульс тела в начальный момент времени)
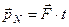 ; (8.3)
; (8.3)
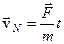 ; (8.4)
; (8.4)
 . (8.5)
. (8.5)
При больших, релятивистских скоростях (  ) выражения (8.1) и (8.2) остаются справедливыми, но меняется определение импульса и энергии:
) выражения (8.1) и (8.2) остаются справедливыми, но меняется определение импульса и энергии:
 (8.6)
(8.6)
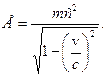 (8.7)
(8.7)
Для безмассовых частиц (фотонов, нейтрино), движущихся со скоростью света, выражения (8.6) и (8.7) становятся неопределенными и записываются иначе.
Поделив (8.6) на (8.7), получим формулу, связывающую энергию и импульс тела (частицы):
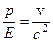 . (8.8)
. (8.8)
С учетом того, что для фотона, например  и
и  , вместо (8.8) имеем
, вместо (8.8) имеем
 . (8.9)
. (8.9)
Возведем (8.7) в квадрат и учтем (8.8):


 . (8.10)
. (8.10)
Для фотона m=0 и 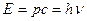 .
.
Формула (8.10) пригодна для всех тел (частиц), в том числе и для частиц с нулевой массой.
Кинетическая энергия в СТО определяется как разность полной энергии Е и энергии покоя 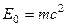 :
:
 . (8.11)
. (8.11)
Представим релятивистский сомножитель в формулах (8.6) и (8.7) в виде степенного ряда:
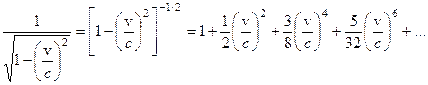
Тогда выражения (6) и (11) можно представить в виде:
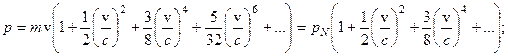 (8.12)
(8.12)
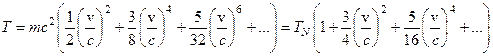 . (8.13)
. (8.13)
Относительная погрешность при использовании в расчете ньютоновских формул:
 ; (8.14)
; (8.14)
 . (8.15)
. (8.15)
Если относительная погрешность задана, то по формулам (8.14) и (8.15) можно рассчитывать наибольшую скорость v (или v/с), до которой можно пользоваться формулами ньютоновской механики (8.3)-(8.5).
Запишем теперь релятивистские формулы, соответствующие ньютоновским формулам (8.3)-(8.5). Возводя в квадрат левую и правую части выражения (8.6), имеем:
 ;
; 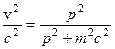 .
.
Но релятивистский импульс, подобно ньютоновскому, при  и
и  линейно зависит от времени:
линейно зависит от времени:
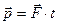 . (8.16)
. (8.16)
Значит,
 . (8.17)
. (8.17)
С учетом формулы (8.10) получим
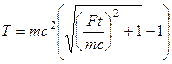 . (8.18)
. (8.18)
Примерные графики, отвечающие соотношениям (8.3)-(8.5) (пунктир) и (8.16)-(8.18), показаны на рис. 8.1.

Рис. 8.1.
Из первого графика следует, что ньютоновский импульс, как и релятивистский, при постоянной силе может стать с течением времени сколь угодно большим. При t=t1 в нерелятивистском случае v=с и далее при 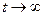 скорость возрастает до бесконечности.
скорость возрастает до бесконечности.
Исследуем выражения (8.17) и (8.18). При 
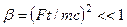 . Используя известные формулы приближенных вычислений
. Используя известные формулы приближенных вычислений  и
и  , легко показать, что в начале движения, пока скорость остается много меньше скорости света, вместо формул (8.17) и (8.18) можно пользоваться формулами (8.4) и (8.5). При
, легко показать, что в начале движения, пока скорость остается много меньше скорости света, вместо формул (8.17) и (8.18) можно пользоваться формулами (8.4) и (8.5). При 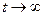
 и
и  , т.е. скорость не может превысить скорость света, а кинетическая энергия неограниченно возрастает, но несколько медленнее, чем в механике Ньютона.
, т.е. скорость не может превысить скорость света, а кинетическая энергия неограниченно возрастает, но несколько медленнее, чем в механике Ньютона.
Таким образом, механика Ньютона - это предельный случай релятивистской механики при  , а при малых скоростях релятивистские формулы переходят в ньютоновские.
, а при малых скоростях релятивистские формулы переходят в ньютоновские.
Рассмотрим теперь релятивистский аналог закона Ньютона - динамическое уравнение частицы, движущейся со скоростью, приближающейся к скорости света в вакууме.
Релятивистский аналог закона Ньютона можно получить из следующих соображений. Подставим в уравнение 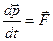 релятивистский импульс
релятивистский импульс  и возьмем производную по времени:
и возьмем производную по времени:
 . (8.19)
. (8.19)
Второе слагаемое в полученном уравнении умножим и разделим на с2. С учетом релятивистского выражения для полной энергии имеем

Но изменение энергии в единицу времени равно работе внешней силы  в единицу времени, т.е.
в единицу времени, т.е.
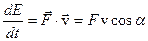 ,
,
где 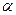 - угол между векторами
- угол между векторами  и
и  .
.
С учетом сказанного перепишем (8.19) в виде
 (8.20)
(8.20)
В общем случае оказывается, что векторы  и
и  не совпадают по направлению. Лишь в двух частных случаях
не совпадают по направлению. Лишь в двух частных случаях 
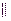
 :
:
1)  и
и 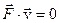 ;
;
2) 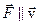 и
и  .
.
В первом случае уравнение (8.20) приобретает вид
 (8.21)
(8.21)
Величина  является мерой инертности в случае, если
является мерой инертности в случае, если  . Обозначив ее
. Обозначив ее 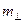 («поперечная масса»), приводим уравнение (8.21) к «ньютоновскому» виду:
(«поперечная масса»), приводим уравнение (8.21) к «ньютоновскому» виду:
 . (8.22)
. (8.22)
Во втором случае уравнение (8.20) примет вид

Или:
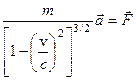 . (8.23)
. (8.23)
Величина 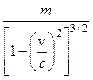 является мерой инертности, когда
является мерой инертности, когда  . Обозначим ее
. Обозначим ее 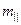 («продольная масса») и запишем уравнение (8.23) в «ньютоновском» виде:
(«продольная масса») и запишем уравнение (8.23) в «ньютоновском» виде:
 .
.
При решении задач уравнение (8.20) часто записывают в проекции на нормаль и касательную к траектории:
 ,
,
 .
.
В общем случае, когда угол между векторами  и
и  произвольный, вообще нельзя ввести скалярную величину, являющуюся коэффициентом пропорциональности между силой и ускорением и называемую релятивистской массой. В таком случае вводится тензор масс, компоненты которого можно рассчитать по формуле:
произвольный, вообще нельзя ввести скалярную величину, являющуюся коэффициентом пропорциональности между силой и ускорением и называемую релятивистской массой. В таком случае вводится тензор масс, компоненты которого можно рассчитать по формуле:
 ,
,
где  ,
, 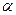 ,
, 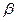 , = 1, 2, 3.
, = 1, 2, 3.
Как видим, продольная и две поперечные массы являются главными значениями этого тензора.
При 

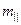
 , где m - масса покоя, т.е. ньютоновская масса, являющаяся мерой инертных свойств тела (частицы), одинаковая во всех ИСО.
, где m - масса покоя, т.е. ньютоновская масса, являющаяся мерой инертных свойств тела (частицы), одинаковая во всех ИСО.
 Необходимо подчеркнуть, что продольная и поперечная масса не являются внутренними характеристиками частицы, а только лишь обозначениями коэффициента пропорциональности в формуле, связывающей ускорение и силу. Масса частицы инвариантна и не зависит от скорости.
Необходимо подчеркнуть, что продольная и поперечная масса не являются внутренними характеристиками частицы, а только лишь обозначениями коэффициента пропорциональности в формуле, связывающей ускорение и силу. Масса частицы инвариантна и не зависит от скорости.
Пусть теперь частица (q - заряд, m - масса) влетает со скоростью  в однородное магнитное поле перпендикулярно его силовым линиям (рис. 8.2). Индукция магнитного поля равна
в однородное магнитное поле перпендикулярно его силовым линиям (рис. 8.2). Индукция магнитного поля равна 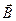 . В этом случае на частицу действует магнитная сила Лоренца
. В этом случае на частицу действует магнитная сила Лоренца
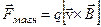 .
.
Модуль этой силы  . Направление
. Направление 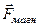 определяется с помощью правила левой руки (рис 8.2). Поскольку
определяется с помощью правила левой руки (рис 8.2). Поскольку 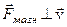 , то эта сила не меняет скорость
, то эта сила не меняет скорость  по направлению. И если скорость частицы приближается к скорости света, то для описания движения частицы следует использовать релятивистское уравнение (8.20) или, поскольку в данном случае
по направлению. И если скорость частицы приближается к скорости света, то для описания движения частицы следует использовать релятивистское уравнение (8.20) или, поскольку в данном случае 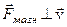 , уравнение (8.21). В проекции на нормаль к траектории
, уравнение (8.21). В проекции на нормаль к траектории
 (8.24)
(8.24)
Сокращая на  и учитывая выражение для релятивистского импульса, получим формулу, связывающую импульс р с радиусом кривизны траектории R:
и учитывая выражение для релятивистского импульса, получим формулу, связывающую импульс р с радиусом кривизны траектории R:
 . (8.25)
. (8.25)
Решая уравнение (8.24) относительно  , можно выразить скорость частицы через радиус кривизны траектории:
, можно выразить скорость частицы через радиус кривизны траектории:
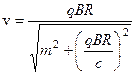 . (8.26)
. (8.26)
В тех случаях, когда  , можно положить
, можно положить  . Если это сильное неравенство имеет противоположный знак, то движение описывает ньютоновской механикой.
. Если это сильное неравенство имеет противоположный знак, то движение описывает ньютоновской механикой.
Дата добавления: 2015-05-16; просмотров: 985;
