Упругие столкновения частиц

Анализ треков частиц, полученных с помощью методик, описанных выше, позволяет отожествить частицу или понять характер ядерного взаимодействия. Анализ проводится с использованием законов сохранения, в частности, законов сохранения энергии и импульса.

Рассмотрим нецентральное (косое) упругое столкновение частицы массой М с неподвижной частицей массой m (рис. 7.9). Обозначим скорость налетающей частицы до столкновения 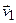и после столкновения 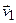’. Соответственно скорости второй частицы до и после взаимодействия пусть будут 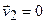и ’.

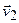На рис. 7.10 показана диаграмма столкновения. Угол 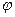называется углом рассеивания, угол 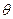- углом отдачи.

Закон сохранения импульса запишем в виде

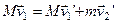. (7.1)

Закон сохранения энергии (частица нерелятивистская):

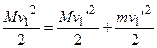. (7.2)

Перепишем векторное уравнение (7.1) в проекциях на координатные оси (х - горизонтальная ось, у - вертикальная ось, на рис. 7.9 и 7.10 оси не показаны):

;

.

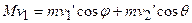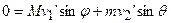Отсюда находим

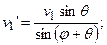
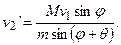
Подставим полученные выражения в (7.2). Получим

;

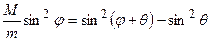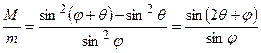(7.3)

( ).

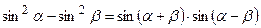Из полученного соотношения следует, что измерив углы 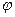и 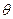, можно рассчитать отношение масс сталкивающихся частиц, а если одна из масс известна, то можно найти другую. Понятно, что соотношение (7.3) можно использовать только в том случае, когда сталкивающиеся частицы не вступают в ядерную реакцию.