Законы радиоактивного распада

Основное предположение, из которого вытекает согласующийся с опытом закон изменения во времени числа радиоактивных ядер (так называемый закон радиоактивного распада), состоит в том, что вероятность распада любого ядра, находящегося в определенном энергетическом состоянии не изменяется со временем. Отсюда следует, что в любой момент времени t число распадов в единицу времени -dN/dt пропорционально числу имеющихся радиоактивных ядер N(t), то есть

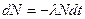. (3.1)

(знак минус означает, что общее число радиоактивных ядер уменьшается с течением времени).

Коэффициент пропорциональности 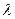, называемый постоянной распада, представляет собой вероятность распада ядра за единицу времени. Интегрирование соотношения (3.1) приводит к выражению:

, (3.2)

где N₀ - число радиоактивных ядер в некоторый произвольный момент времени, принятый за начало отсчета, 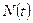- количество радиоактивных ядер, оставшихся в источнике к моменту времени t. Таким образом, число еще не распавшихся радиоактивных ядер уменьшается по экспоненциальному закону. Точно такой же зависимостью от времени характеризуется и число распадов в единицу времени А(t), называемое активностью[1] образца. Действительно,

, (3.)

где А₀ - активность в начальный момент времени t=0. Зная функцию распределения во времени радиоактивных ядер (3.2), можно вычислить среднее время жизни 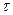радиоактивного ядра:

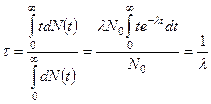. (3.4)

Отсюда следует, что среднее время жизни есть время, в течение которого число радиоактивных ядер, а также активность образца уменьшаются в е раз. На практике оказывается более удобной другая временная характеристика распада - период полураспада Т, который определяется как время, в течение которого число радиоактивных ядер или активность образца уменьшается вдвое, то есть

. (3.5)

Отсюда вытекает следующая связь между периодом полураспада, постоянной распада и средним временем жизни:

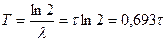. (3.6)

Процесс образования радиоактивного вещества (например, при облучении стабильных ядер нейтронами) называется активацией. Число радиоактивных ядер Q, возникающих в данном объеме вещества в единицу времени, пропорционально числу стабильных ядер в единице объема п облучаемой мишени, объему мишени V, числу частиц (нейтронов) 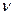, пересекающих в единицу времени площадь мишени, и эффективному сечению 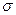ядерной реакции, в результате которой появляются радиоактивные ядра (так называемое сечение активации), то есть

. (3.7)

Так как одновременно с образованием радиоактивных ядер происходит их распад, то изменение числа радиоактивных ядер в единицу времени будет равно:

, (3.8)

где N - число радиоактивных ядер. Решение уравнения (3.8) дает закон изменения во времени числа радиоактивных ядер:

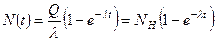. (3.9)

Видно, что величина N(t) стремится в пределе к постоянному значению N(t)_Н, называемому активацией насыщения, когда число образующихся радиоактивных ядер равно числу распадающихся, так что dN/dt = 0. Отсюда

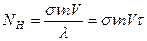. (3.10)

Таким образом, активация насыщения соответствует числу радиоактивных ядер, образующихся за время облучения, равное их среднему времени жизни. Активность образца при облучении постоянным потоком нейтронов дается выражением:

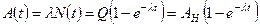, (3.11)

где А_Н - максимально достижимая активность, или активность насыщения. Из формулы (3.10) следует, что предельное число радиоактивных ядер в образце N_Н (активация насыщения) тем выше, чем больше скорость их образования Q, а при данном значении Q - чем больше их время жизни. Предельная же активность образца А_Н (активность насыщения не зависит от периода полураспада и равна скорости образования радиоактивных ядер Q. Примеры кривой активации, т. е. зависимости активности образца от времени облучения исходного материала нейтронами, и кривой распада, т. е. зависимости активности образца от времени после прекращения облучения по достижении активации насыщения, приведены на рис. 3.1.

Отметим, что если за время, равное периоду полураспада, распадается половина начального числа радиоактивных ядер, то при активации за тот же интервал времени образуется число радиоактивных ядер, равное половине активации насыщения. За время, в 5 раз превышающее период полураспада, распадается около 97% имевшихся первоначально радиоактивных ядер, а в случае активации образуется около 97% числа радиоактивных ядер, соответствующих активации насыщения.

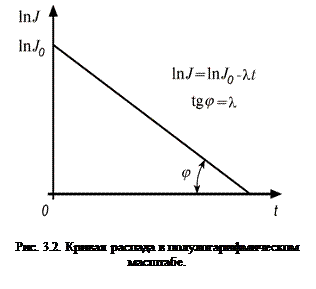
В полулогарифмическом масштабе кривая распада (3.2) или (3.3) представляет собой прямую линию, угол наклона которой определяется постоянной распада (см. рис. 3.2).

В ряде случаев изменение активности образца во времени не подчиняется экспоненциальному закону (3), что является указанием на наличие нескольких сортов радиоактивных ядер с различными периодами полураспада. Причины их появления могут быть различные:

1) Облучаемое вещество может состоять из смеси нескольких стабильных изотопов, которые после захвата нейтрона превращаются в соответствующее число радиоактивных изотопов, каждый из которых распадается независимо от других со своим периодом полураспада. Если имеет место смесь двух независимых радиоактивных веществ, уравнение кривой распада запишется:

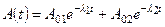, (3.12)

где А₀₁ и А₀₂ - активности изотопов в начальный момент времени.

2) Облучаемое вещество представляет собой один изотоп. В результате захвата нейтрона также образуется один радиоактивный изотоп; однако образующиеся в результате его распада ядра, в свою очередь, испытывают распад, и так далее, то есть возникает цепочка распадов, или радиоактивный ряд. Запишем исходные уравнения, определяющие изменение числа радиоактивных ядер каждого члена ряда, имея в виду, что баланс количества ядер каждого дочернего вещества определяется скоростью собственного распада, пропорциональной числу имеющихся ядер этого вещества, и скоростью образования, равной числу распадов предшествующего материнского вещества в единицу времени:

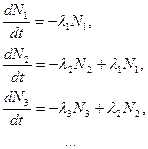(3.13)

Решение уравнений (3.13) для простейшего случая двух последовательных распадов имеет вид:

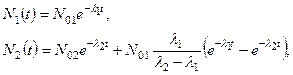(3.14)

где N₀₁ и N₀₂ - начальные количества ядер материнского и дочернего радиоактивных веществ, например, в момент прекращения облучения. Отметим, что первое слагаемое в выражении для N₂(t) описывает изменение во времени числа ядер дочернего вещества, уже существовавших до момента t = 0 и равного в этот момент величине N₀₂; второе слагаемое - это число ядер дочернего вещества, появившихся в результате распада материнского начиная с момента t = 0. Из этого, в частности, следует, что изменение во времени какой-то части радиоактивных ядер происходит в соответствии с экспоненциальным законом (3.2) независимо от появления в дальнейшем новых количеств таких лее радиоактивных ядер, и полное число радиоактивных ядер всегда равно сумме ядер, сохранившихся к данному моменту времени от всех источников радиоактивности.

3) В результате ядерной реакции, идущей, например, под действием нейтронов на ядрах вещества мишени, состоящего из одного стабильного изотопа, образуются ядра - изомеры, имеющие одинаковый нуклонный состав, но находящихся в разных энергетических состояниях: в основном состоянии и в возбужденном - метастабильном (так называемом изомерном). Изомерным является возбужденное состояние ядра, имеющее сравнительно большой период полураспада (принята оценка Т_1/2 > 10⁸ с) и момент количества движения I,обычно отличающийся от моментов нижележащих состояний (как правило, 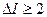). Переходы из изомерных состояний в другие состояния ядра - изомерные переходы происходят путем испускания 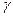-квантов или электронов внутренней конверсии (т. е. электронов оболочки атома, которым передана энергия возбуждения ядра за вычетом энергии связи). Период полураспада изомерного состояния зависит от энергии изомерного перехода (возрастая с уменьшением этой энергии) и от разности моментов количества движения 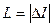состояний ядра, между которыми этот переход происходит, возрастая с увеличением L. Так, если энергия изомерного перехода невелика (Е ~ 100 кэВ), то период полураспада изомерного состояния для излучения с L=3 исчисляется часами, а для L=4 - годами. В одном и том же ядре может быть несколько изомеров. Явление изомерии весьма распространено, в настоящее время известны сотни изомеров.

При наличии изомеров может иметь место цепочка распадов: первое её звено - переход из изомерного состояния в нижележащее состояние ядра (часто этим состоянием является основное), второе звено - радиоактивный распад получающегося состояния. Закономерности распадов в этом случае также определяются системой уравнений, аналогичной (3.13). Если ядра в основном состоянии образуются не только при распаде изомера, но и непосредственно в ядерной реакции, то величина N₀₂ в решении (3.14) представляет собой суммарное количество ядер в основном состоянии в момент прекращения облучения, образовавшееся как в результате распадов метастабильного состояния, так и непосредственно в процессе активации.