Предмет экологии насекомых 12 страница

Увеличим площадь пробы вдвое. Тогда число потенциальных мест в пробе будет равно S/s = 2.

Тогда возможны следующие три ситуации при взятии пробы: или в пробе 2 особи, или в пробе 1 особь, или проба пуста. Вероятность каждой из этих ситуаций определяется коэффициент уравнения

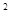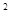(p + q) = p + 2pq + q 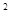, т.е. 1:2:1.

Теперь рассмотрим случай, когда из каждых четырех территорий одна занята, а три свободны, т.е. вероятности p = 1/4, q = 3/4. Тогда, если S=2s, то по две особи будут в 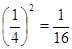от всего количества проб, по одной в 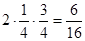, а полностью будут пустыми - в 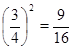, т.е. их соотношение будет выражено числами 1:6:9.

Как правило, площадь пробы существенно превышает площадь территории, занимаемой одной особью. Если соотношение этих площадей n, то эмпирическое распределение будет соответствовать последовательным членам развернутого уравнения (p + q) , т.е. биномиального распределения (бином Ньютона).

Случайное размещение

Такое размещение возникает в том случае, если среда более или менее равномерна и особи не испытывают ни притяжения друг к другу, ни отталкивания. Именно так распределены в муке при сравнительно небольшой плотности популяции личинки большого мучного хрущака Tenebrio molitor L., а также личинки жуков–стафилинид на поверхности почвы.

Остановимся далее на моделировании случайного размещения. Биномиальное распределение, рассмотренное в предыдущем разделе, предусматривает достаточно высокую плотность популяции, когда число незанятых территорий относительно мало. Если же изучаемый объект редок (p 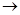0) и распределен по потенциальным территориям случайным образом, а само число этих территорий велико ( 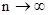), то биномиальное распределение переходит в распределение редких событий (распределение Пуассона). При этом вероятность обнаружения в пробе того или иного количества насекомых будет зависеть только от размера пробы, но не от того, где именно эта проба взята.

Согласно формуле Пуассона, ожидаемое число проб 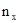с количеством особей x равно:

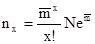
где N – общее количество всех взятых проб, 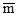– среднее число особей на одну пробу, е – основание натуральных логарифмов (е 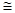2,71828) , х!– икс–факториал – произведение ряда натуральных чисел, например 3! = 1·2·3.

В случае распределения Пуассона дисперсия и арифметическая средняя примерно равны, т.е.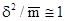

Если же вероятность нахождения объекта достаточно высока, то упомянутое выше биномиальное распределение превращается в широко известное из статистики нормальное распределение (распределение Гаусса). В переходных случаях максимум кривой распределения обычно смещен в сторону меньших значений признака (влево), так как относительно велико число проб с небольшим количеством особей (рис.21). При малых же пробах максимум кривой распределения смещается на 0 (т.е. большинство проб – пустые) и от кривой остается только нисходящая ветвь.

Агрегированное размещение

Размещение этого типа наиболее обычно в природе. Насекомые скапливаются на участках, где для них особенно благоприятен микроклимат, имеются их кормовые растения или жертвы. Кроме того, многие насекомые привлекают друг друга благодаря наличию так называемых агрегационных феромонов (М.Барбье, 1978). Степень агрегированности может зависеть от погоды, сезона и времени суток. Насекомые в малоактивном состоянии чаще образуют скопления в благоприятных для переживания местах. Последнее в первую очередь относится к хищным насекомым.

Рис.21. Пуассоновское распределение вероятности (по А.А. Шарову, 1984)

Агрегированное пространственное размещение особей может быть различных типов, а именно: группы могут быть сходными или различными по численности, размещение особей в пределах группы является или случайным, или равномерным. Кроме того, в ряде случаев группы могут объединяться в скопления групп. Соответственно, эти размещения описываются различными теоретическими кривыми. В любом случае, однако, здесь коэффициент дисперсии всегда больше единицы.

Один из конкретных примеров агрегированного размещения дают личинки комаров–долгоножек, обитающие в почве. Они скапливаются группами примерно по 30 особей. На каждую особь приходится по 1–2 см 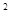, а на 1 м 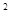можно найти около 10 таких скоплений. Отдельные особи могут оказываться и в пространстве между группами.

Как уже отмечалось выше, уровень агрегированности популяции насекомых можно определить двумя путями, либо с помощью индексов агрегированности, показывающих степень неравномерности размещения, либо проверкой соответствия данного размещения определенному теоретическому распределению, что, конечно, является более точным описанием.

Однако применение того или другого способа будет корректным только после предварительного анализа размещения. Дело в том, что полученная нами картина распределения может существенно зависеть от размера пробы, в частности, от того, меньше или больше она, чем средний размер скоплений.

Для проверки целесообразно взять серии проб разного размера, например, при исследовании почвенной фауны 40 проб по 0,25 м 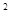, 20 проб по 0,5 м 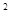и 10 проб по 1 м 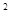(А.В.Смуров, 1975). Для каждой из серий необходимо определить среднеарифметическую величину сбора данных насекомых на одну пробу ( 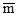) и дисперсию ( ).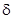

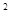По виду зависимости дисперсии от средней можно выбрать индекс агрегированности и теоретическое распределение для описания размещения насекомых. В одном случае коэффициент дисперсии (дисперсия, деленная на среднеарифметическую) не будет зависеть от средней, т.е. будет почти одной и той же величиной, независимо от размера пробы, в другом же – будет сначала линейно возрастать с увеличением средней (размера пробы), отходя от единицы на оси ординат (рис.22). При достижении пробой величины скопления насекомых на графике имеет место точка перегиба кривой и далее с увеличением пробы коэффициент дисперсии почти не меняется.

В первом случае в качестве индекса агрегированности можно выбрать сам коэффициент дисперсии. Теоретические распределения, соответствующие данному случаю – распределения Неймана (J.Neyman, 1939) и Томас (M.Thomas, 1949). Эти распределения имеют место, когда размер пробы значительно больше скопления насекомых. В общем такие случаи редки в энтомологической практике и мы не будем здесь далее на них останавливаться.

Гораздо чаще коэффициент дисперсии возрастает с увеличением пробы, т.е. скопления велики по сравнению с площадью, охватываемой пробой. В этом случае необходимо использовать иные, чем коэффициент дисперсии, индексы агрегированности. Перечислим некоторые из них.

Л.Р.Тейлор (L.R.Taylor, 1961) на основании изучения размещения на местности многих видов насекомых предложил следующую эмпирическую формулу:

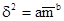
Рис.22. Зависимость коэффициента дисперсии от средней для ряда реальных размещений, описываемых различными теоретическими распределениями: А – Неймана и Томас; Б – отрицательным биномиальным и трехпараметрическим; В – гипотетическим реальным при непрерывном увеличении размера пробы и соответственном увеличении средней. Квадратами разного размера под осью абсцисс показаны относительные размеры проб. При малом размере проб здесь возможно использовать отрицательное биномиальное и трехпараметрическое распределения, при большом – распределения Неймана и Томас. При средних размерах пробы теоретическое распределение не может быть подобрано (заштрихованная область) (по А.В. Смурову, 1975)

где а – величина, зависимая от размера пробы, а b – индекс уровня агрегированности. Чем больше b, тем выше этот уровень. Коэффициенты а и b можно вычислить, логарифмируя приведенное выше уравнение:

log 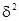=log a + b log .

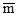Так как это уравнение с двумя неизвестными, необходимо провести две серии учетов с разными размерами проб.

Другая тоже эмпирическая формула была предложена японскими исследователями (S.Ivao, E.Kuno, 1968):

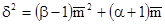
В этой формуле коэффициент 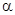определяет, что является основным параметром анализируемого размещения: отдельные особи или их скопления, а коэффициент β показывает агрегированность этих компонентов в пространстве.

Чаще, по крайней мере в отечественной литературе, используют тоже эмпирический индекс агрегированности М. Мориситы (M.Morisita, 1959):

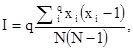
где I – индекс агрегированности, q – общее число проб данного размера, 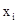– реальное число особей в каждой пробе, N – общее (суммарное) число особей во всех q пробах. Этот показатель при агрегированном размещении больше единицы.

Агрегированное размещение во многих случаях хорошо описывается, так называемым отрицательным биномиальным распределением. Поэтому в качестве индекса целесообразно использовать константу К этого распределения. Ее можно подсчитать по следующей формуле:

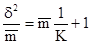
Приближение К к нулю свидетельствует о большой агрегированности популяции. Наоборот, чем больше К, тем распределение сборов по пробам ближе к случайному. Так, по данным В.Е. Уотерса (V.E.Waters, 1959), при низкой плотности популяции Choristoneura fumiferana константа К изменяется в пределах 1–5 (агрегированное размещение). При более высокой плотности популяции их размещение становится все более случайным (значение К в пределах 6 – 50).

Иногда используют также величину С, обратную К:

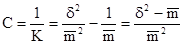
Величина С может быть определена как тангенс угла наклона графика зависимости коэффициента дисперсии от средней (от размера пробы).

Индекс Мориситы и константы отрицательного биномиального распределения связаны друг с другом следующим образом:

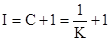
А.В.Смуров (1975) предложил в качестве индекса агрегированности 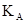следующую формулу:

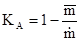
где 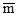– средняя плотность популяции в пределах всей занимаемой ею территории, включая незаселенные пространства, 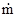– средняя плотность в местах скоплений. При полностью случайном распределении этот индекс равен нулю, а при максимальной агрегированности он будет стремиться к единице. Индекс А.В.Смурова имеет наглядный биологический смысл, так как показывает, какая часть общей площади не занята скоплениями. Связь между этим индексом и предыдущими можно выразить следующим образом:

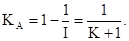
Мы уже упоминали выше, что в случае агрегированного размещения особей коэффициент дисперсии сначала увеличивается при увеличении размера пробы (соответственно и увеличении среднего количества особей в пробе). Эти изменения связаны с соотношением размера пробы и средней площади, занимаемой скоплением особей. В принципе здесь мы всегда имеем дело, как минимум, с "двойным" размещением: размещением скоплений на местности и размещением самих особей внутри скоплений. Возможно и образование групп скоплений.

Известны два теоретических распределения, соответствующих данной ситуации. Это отрицательное биномиальное распределение (С.J.Bliss, R.A.Fischer, 1953; рис.23) и трехпараметрическое распределение (А.В. Смуров, 1975). На практике чаще используют сравнение эмпирических данных с расчетом по формуле отрицательного биномиального распределения (эта формула является лишь хорошей апроксимацией, более подробно это изложено в книге А.В.Смурова и Л.В.Полищука, 1989) Согласно формуле отрицательного биномиального распределения вероятность обнаружения в пробе x особей

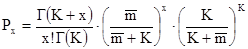
где Г(К+х) и Г(К) – гамма–функции, т.е. факториалы дробных чисел, К – константа отрицательного биномиального распределения, а 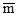– среднее количество особей в пробах. Гамма–функция может быть вычислена по следующей приближенной формуле:

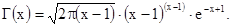
Конкретный пример расчета отрицательного биномиального распределения дан А.А.Захаровым и др. (1987) (На стр.204 цитируемой книги допущена опечатка – вместо м = (xp)/(І – p) следует читать 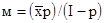). Как уже отмечалось выше, А.В.Смуровым было предложено так называемое трехпараметрическое распределение, основанное на следующих параметрах: общей средней плотности популяции, плотности в пределах скоплений и плотности вне скоплений. Согласно этому распределению, как в случае отрицательного биномиального распределения, коэффициент дисперсии также меняется в зависимости от величины пробы.

Рис.23 Отрицательное биноминальное распределение вероятности (по А.А.Шарову, 1984)

Все эти теоретические распределения могут переходить друг в друга при существенном изменении их параметров. Поэтому, если нет уверенности в справедливости какой-либо определенной модели распределения, рекомендуется использовать так называемое трехпараметрическое распределение Пуассона с нулями (А.В. Голубев, Г.Э. Инсаров, В.В. Страхов, 1980), являющееся наиболее универсальным.

3. УЧЕТ ЧИСЛЕННОСТИ НАСЕКОМЫХ

Определение численности насекомых исключительно важно не только в теоретическом отношении, но и в практических целях. Современная защита растений основана на управлении естественными популяциями фитофагов и энтомофагов при минимальном вмешательстве человека в их естественный баланс. Истребительные мероприятия, в первую очередь использование специально разведенных энтомофагов, а также возбудителей вирусных, бактериальных и грибковых заболеваний и, в последнюю – химических средств защиты растений, должны проводиться только в том случае, если природный баланс настолько сильно нарушен, что без вмешательства пропадет существенная часть урожая. Подобный контроль за состоянием агроценоза невозможен без регулярных учетов численности насекомых. Однако необходимо подчеркнуть, что, в отличие от крупных животных, например зубров или амурских тигров, полностью учесть численность насекомых, входящих в данную популяцию, за редчайшими исключениями, невозможно. Поэтому при учетах численности насекомых всегда используют косвенные методы, позволяющие сделать лишь приближенное заключение о численности их популяции.

Строго говоря, значение насекомых данного вида в жизни биоценоза определяется не его суммарной численностью, а количеством насекомых на единицу площади биотопа, т.е. плотностью популяции. В практике защиты растений как показатель плотности часто используют среднее количество особей данного вида в расчете на одно растение. Очевидно, что оба эти показателя легко переводятся друг в друга, так как в сельскохозяйственных угодьях на одно растение приходится определенная площадь. В лесной энтомологии как показатель плотности обычно используют процент деревьев, заселенных данным фитофагом. В последнее время аналогичный показатель, требующий меньше усилий для учета,– процент растений, на которых обнаружен фитофаг – используют и в сельскохозяйственной практике. Для каждого вида можно установить определенную связь между процентом заселенных деревьев и средним числом особей на дерево (А.И.Воронцов, А.В.Голубев, Е.Г. Мозолевская, 1983).

Применяются и более специальные показатели плотности. Например, для сосновых лубоедов целесообразно определять "экологическую плотность" – число особей на единицу поверхности кормового субстрата, (коры) отдельно жуков родительского поколения, яиц и жуков молодого поколения, а также плотность поселения – число семей или число маточных ходов лубоедов на единицу поверхности кормового субстрата (Е.Г.Мозолевская, 1983).

Конечно, нет полностью универсальных методов учета, пригодных для любых насекомых на любых стадиях их развития (С.П. Расницын, 1978). Но некоторые методы позволяют все же учитывать представителей многих видов и даже отрядов насекомых (визуальный учет на растении, кошение энтомологическим сачком). При выборе метода учета следует также обращать внимание на качество получаемого материала. Так, при визуальном учете возможны ошибки в определении видового состава. При сборе насекомых светоловушкой повреждается значительная часть насекомых.

Подробное обоснование и описание разных методов учета численности насекомых дано в книге Саузвуда (T.R.E. Southwood, 1966).

Простейшие методы учета численности

Мы уже отмечали нереальность определения абсолютной численности насекомых в пределах того или иного биотопа. Можно учесть, например, в одной роще число поющих самцов какого-либо вида кузнечиков, но мы не узнаем таким образом, сколько еще тех самцов, которые по тем или иным причинам не пели во время учета. Аналогично учет всех летающих на поляне бабочек не может быть принят за полный. Он не является даже и относительным, так как на следующий день мы обнаружим в зависимости от погоды и физиологического состояния бабочек на той же поляне другое их количество, даже если их численность сохранилась прежней и не было ни эмиграции, ни иммиграции.

В энтомологии иногда применяют учет на линейных маршрутах (маршрутный учет). Очевидно, что данный метод применим только для учета крупных и хорошо заметных насекомых. Мы использовали этот метод, наблюдая крупных чернотелок в песчаной пустыне с небольшим количеством растений, где практически гарантирован учет на поверхности всех жуков данного вида на расстоянии до 5 м от наблюдателя. Тогда общая плотность популяции чернотелок, находящихся на поверхности, может быть определена по формуле:

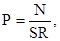
где P – плотность популяции в расчете на 1 м 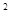, N – суммарное число насекомых, обнаруженных на обследуемой поверхности вдоль маршрута (только по одной стороне – слева или справа от наблюдателя), S – длина маршрута, R – ширина обследуемой поверхности – в нашем случае 5 м.

Маршрутный учет может оказаться полезным при изучении населения бабочек, летающих днем. Однако, как отмечалось выше, такой учет будет очень приблизительным из-за изменений процента бабочек, находящихся в активном состоянии, а также из-за мигрирующих особей, численность которых может во много раз превышать численность локальной популяции, но они могут как остаться в этом районе, так и пролететь дальше. Конечно, сравнивать численность разных видов или одного вида в разные годы можно только по учетам за очень длительный срок. Результаты, полученные в отдельные случайно выбранные дни или даже в один и тот же день, но в разные годы, очевидно, невозможно интерпретировать.

Для учета численности в небольших относительно изолированных биотопах был предложен так называемый метод исчерпывания. При таком учете необходимо, чтобы эмиграция и иммиграция насекомых были очень незначительными, что достигается либо при наблюдениях за относительно медленно передвигающимися насекомыми, либо при искусственных препятствиях для перемещения, например, постановке загородок, которые не могут перейти нелетающие насекомые. Кроме того, исходно предполагается, что эффективность метода сбора примерно одинакова при разных уровнях численности популяции. Предположим, что в первый улов насекомых на обследуемой территории мы выловили долю их населения, равную р. Если вся популяция состоит из а насекомых, то в этом улове будет ар особей, а останется невыловленным а(1 – р). При следующем вылове останется уже а(1 – р) 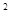, при х–ном вылове будет поймано ра (1 –р) 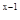особи, а останется а(1– р) 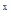(А.А.Любищев, 1958). С каждым уловом его абсолютная величина будет снижаться. Формулы учета методом исчерпывания следующие:

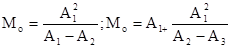или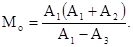

Л.Н.Медведев (1971) предлагает эти формулы для учета с помощью энтомологического кошения. Однако на практике учет таким способом осуществим далеко не для всех объектов. Так, А.А.Любищев (1958) показал, что даже при очень тщательном обкашивании растительности сачком улавливается всего около 1 % популяции, поэтому следующие друг за другом учеты на одном и том же месте совсем не обязательно покажут снижение численности на обследуемом участке. Кроме того, результаты учетов существенно зависят от погоды и времени суток. Производить же учеты сразу один за другим нельзя, так как после обкашивания сачком неизбежно нарушается распределение насекомых на растении.

Метод исчерпывания был успешно применен А.И.Кудриным (1971) при учете численности нелетающих или редко летающих жужелиц. Этот автор огораживал участок, заселенный жужелицами, специальным заборчиком, чтобы свести к нулю эмиграцию и иммиграцию. Вылов же на участке проводился на протяжении многих суток с помощью ловушек Барбера (банок, вкопанных в землю на уровне ее поверхности).

Также далеко не во всех случаях применим метод маркировки и последующего отлова. Суть этого метода сводится к следующему. На обследуемом ограниченном участке вылавливают определенное число особей. Их метят, опять выпускают в природу, дожидаются, пока они равномерно распределятся по биотопу, а потом проводят повторный вылов. Тогда:

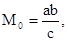
где М 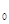– численность особей на всем участке, а – число пойманных и вновь выпущенных особей, b – число всех пойманных особей, с – число вновь пойманных меченых особей. Очевидно, что при таком учете необходимо соблюдение, по крайней мере трех условий: 1) меченые особи после выпуска распределяются по всему участку случайно; 2) практически отсутствует эмиграция и иммиграция и 3) поимка и мечение насекомых никак не отражаются на их активности.

Несколько слов о нанесении меток на насекомых. Чаще всего применяют быстро сохнущие и несмываемые нитрокраски или даже лак для ногтей. Бабочек метят, наклеивая на крыло кружок тончайшей фольги, который видно издалека по блеску. На неопушенных надкрыльях некоторых жуков метки почти не держатся, поэтому их метят, прокалывая надкрылья специальным пробойником или ампутируя небольшой кусочек надкрылья. Возможно нанесение меток с помощью радиоактивных изотопов. Конечно, мечение насекомых применяется не только для учета их численности, но и для других целей, прежде всего для изучения миграций.

Сложен также вопрос о сроке, через который надо проводить второй сбор насекомых. Этот интервал времени не может быть слишком большим, так как за это время могут появиться новые особи, погибает часть меченых, происходит в какой-то мере эмиграция и иммиграция. Слишком же короткий интервал может оказаться недостаточным для равномерного "перемешивания" популяции. Иногда здесь имеют значение и физиологические особенности изучаемых насекомых. Так, при вылове мух цеце на жертве, второго прилета можно ожидать только через определенный срок (C.H.N.Jackson, 1939). Этот автор, применяя различные краски для меток, определил изменения повторного вылова меченых мух на протяжении 6 последующих недель. Полученные им величины выловов, выраженные в логарифмах, располагались на графике по прямой постепенно снижающейся линии, что позволило путем математической интерполяции определить процент вылова меченых особей, который мог бы иметь место в тот день, когда были выпущены меченые особи.

Учет численности популяций с помощью проб

Невозможно учесть всех насекомых на обследуемой территории. В принципе, в этом и нет необходимости, так как для принятия какого-либо практического решения необходимо знать лишь ориентировочное значение плотности популяции, взятое с определенной степенью точности. Иногда вполне достаточна только информация о том, превышает ли средняя плотность какой-то определенный, заранее установленный уровень. Поэтому вместо обследования всей территории подсчитывают численность насекомых на небольших, случайно взятых участках одинакового размера и по таким пробам судят о плотности популяции насекомых на всей территории. В качестве проб могут выступать небольшие количества растительного опада и грунта, взятые с определенных маленьких площадок, отдельно взятые на поле растения, участки коры или отдельные ветки дерева, определенным образом расположенные в кроне (например, на определенной высоте над землей).

Как пробы иногда используют сборы насекомых сачком или какими-либо ловушками. Последнее, однако, нежелательно, так как обычно оказывается невозможным пересчет результатов сбора на реальную плотность, поскольку уловистость, т.е. доля учтенных особей от их общего числа в популяции варьирует в зависимости от погоды, физиологического состояния насекомых, а также от личности учетчика. Правда, по мнению В.Н.Беклемишева (1934), учет с помощью сачка в воде дает достаточно точные результаты, поскольку в такой сачок попадает около 60% общего количества личинок комаров в полосе захвата (уловистость – 0,6)

Иногда определяют такую относительную величину как встречаемость – долю проб, в которых есть насекомые данного вида. Эта характеристика очень удобна, если в качестве пробы используется отдельное растение. Если размеры проб могут быть изменены, то встречаемость будет возрастать с их увеличением.

При определении плотности популяции необходимо сначала решить следующие вопросы:

1. С какой степенью точности мы должны учесть численность?

2. Каков должен быть размер (площадь) пробы?

3. Сколько проб мы должны взять для проведения учета с заданной степенью точности?

4. Как эти пробы должны быть распределены на местности?

Очевидно, что даже при попытке сплошного обследования мы никогда не добьемся 100%–ной точности учета. При любом обследовании всегда остаются в силе ошибки, связанные с несовершенством самого процесса учета. В частности, при почвенно–зоологическом исследовании для всех видов с умеренным уровнем численности ошибка средней при учете лежит в пределах 15 – 40% и редко бывает ниже 10%. По-видимому, реальная точность учетов в сельскохозяйственной практике также не превышает 80%. Бессмысленно добиваться значительного повышения точности выборочного учета за счет увеличения числа или объема проб, если при учете каждой пробы имеют место значительные ошибки. Однако ошибка 20% означает, что в одном случае из пяти мы рискуем принять ошибочное решение.

Размер пробы определяется традицией, размерами и подвижностью учитываемых насекомых и типом их пространственного размещения. Мелкие пробы более равномерно охватывают площадь, на которой проводится учет. С другой стороны, взятие более крупных проб той же суммарной площади менее трудоемко. Рекомендуется подбирать размер почвенной пробы так, чтобы в пробах были десятки, но не единицы и не сотни особей (Э.Макфедьен, 1965). Соответственно, для почвенных насекомых при их линейных размерах около 30 мм площадь пробы должна быть не менее 0,5 м 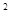, при длине около 10 мм – 0,25 м 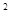. Если же длина тела меньше 10 мм, то можно ограничиться пробами площадью 0,125 м 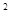. Для учета же, например ногохвосток, могут быть использованы мелкие пробы 5x5 см.