Процес і методи обґрунтування рішень.

Якість прийнятих рішень залежить від того, наскільки ОПР володіє сучасними методами і процедурами наукового їх обґрунтування. А це означає, що необхідно оволодіти методами вибору і прийняття рішень із застосуванням математичних моделей, алгоритмів і процедур аналізу си­туації і синтезу рішення.

Певний скептицизм керівників виробництва і спеціалістів до економіко-математичних методів обґрунтування рішень нерідко пояснюють складністю виробничих процесів, впливом значної кількості некерованих факторів на результати рішень, недосконалістю математичного апарату. З іншого боку фахівці, що розробляють математичний апарат прийняття рішень, нарікають на невміння виробничників правильно поставити за­дачу. Не варто нехтувати жодними із цих аргументів, бо вони мають ре­альні підстави. Плідної взаємодії можна досягнути, якщо фахівці аграр­ного профілю оволодіють методологією і арсеналом ефективних методів обґрунтування рішень. Загальна схема процесу прийняття рішень наведе­на на рис. 1.5.

Рис. 1.5 Загальна блок-схема прийняття рішень

Сукупність методів обґрунтування рішень можна поділити на дві гру­пи: евристичні й аналітичні.

Евристичні методи спираються на досвід та інтуїцію. При цьому про­цеси мислення, в результаті яких генерується рішення, можна подати у ви­гляді кібернетичного «чорного ящика». Тобто внутрішні закономірності, що перетворюють вхідну інформацію у вихідне рішення, не піддаються опису, а ОПР можна порівняти з чарівником або щасливчиком, що вирі­шив задачу невідомим йому самому способом (еврика!).

Аналітичні методи передбачають синтез рішення з використанням математичних моделей і певних алгоритмів. Якість рішення в цьому ви­падку залежить від адекватності моделі, тобто її відповідності реальному об’єкту чи процесу за найбільш важливими властивостями.

Евристичні і аналітичні методи мають певні переваги і недоліки. Так, опора евристики на досвід та інтуїцію не дозволяє вирішувати багатоварі- анті задачі з урахуванням значного числа факторів. Відомо, що людина здат­на оперувати одночасно 5-7 факторами, при цьому часто не враховується багато істотних для процесу факторів. Тому немає гарантії, що прийняте рішення є оптимальним або хоча б задовільним. І все ж, евристичні мето­ди успішно використовуються для вирішення творчих задач вдосконалення виробничих і технічних систем. На даний час розроблені ефективні методи активізації творчого мислення, пошуку нестандартних рішень.

Основними труднощами аналітичних методів є забезпечення адекват­ності моделі, уникнення невизначеності цілей і умов, врахування факто­рів, що не мають кількісного виразу (психологічні, ергономічні та ін.)

Множину моделей прийняття рішень можна умовно класифікувати за схемою (рис. 1.6).

На схемі виділені лише принципово важливі ознаки моделей. Так як практично всі перелічені ознаки є взаємно сумісними і можуть поєдну­ватись у будь-якій комбінації, то число класів моделей буде дорівнювати 2⁵ = 32.

Виділимо найбільш поширені в інженерній практиці аналітичні моде­лі прийняття рішень.

Розрахункові детерміновані моделі характеризуються наявністю од­нієї або сукупності аналітичних залежностей, методики (алгоритму) розрахунку, повною визначеністю умов і змінних факторів. Наявність невизначеності ймовірнісної природи усувається заданням відповідних статистичних характеристик випадкових величин (математичне споді­вання, дисперсія).

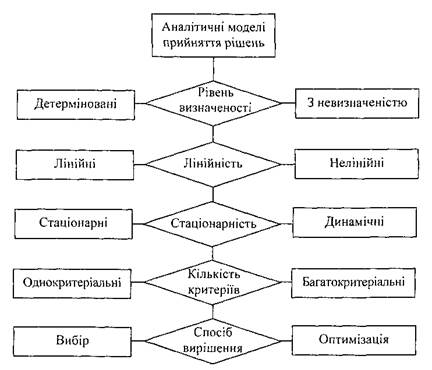
Рис. 1.6. Схема класифікації моделей обгрунтування рішень

Моделі цього класу, як правило, прості, хоча можуть бути трудоміст­кими. Значне скорочення затрат часу на розрахунки досягається при ви­користанні комп’ютерних програм.

В машиновикористанні такі моделі поки що найбільш поширені. Ви­значення потреби в техніці, розрахунок плану механізованих робіт і тех­нічного обслуговування, визначення розмірів площадок для тривалого зберігання техніки і багато інших задач вирішуються за допомогою роз­рахункових детермінованих моделей.

Оптимізаційні моделі передбачають встановлення таких значень керо­ваних змінних, при яких величина критерію є найближчою до цілі з усіх інших можливих рішень у заданій області зміни факторів. Із великої різ­номанітності оптимізаційних моделей виділимо наступні.

Одномірна оптимізація без обмежень характеризується наявністю цільової функції з однією змінною. Такі задачі вирішуються класичними методами знаходження екстремуму функцій, що диференціюються. Зви­чайно, що одномірна оптимізація може використовуватися лише в най­простіших часткових задачах, бо не дозволяє врахувати взаємодії бага­тьох факторів на кінцеве рішення.

Багатомірна оптимізація полягає у знаходженні оптимуму (найкра­щого рішення) функцій з декількома змінними.

У сфері експлуатації МТП задач такого типу є досить багато. Напри­клад, продуктивність МТА може бути виражена як функція параметрів і режиму роботи агрегату (ширина захвату, робоча швидкість, норма вне­сення), польових умов (рельєф, довжина гону, площа поля). З врахуванням взаємозв’язків керованих факторів така функція може мати екстремум.

Значну групу багатомірних функцій складають емпіричні рівняння ре­гресії, за допомогою яких виражається ряд показників.

Лінійне програмування відноситься до класу оптимізаційних методів при наявності обмежень. При цьому змінні фактори входять до цільової функції та обмежень у першій степені. Термін «програмування» запозиче­ний із зарубіжної літератури і відображає процес прийняття рішень, а не розробку програм.

Прикладами задач, що вирішуються методами лінійного програму­вання, є розподіл техніки за видами робіт (завантаження обладнання), оптимальне планування перевезень вантажів (транспортна задача), ефек­тивний розподіл, дефіцитних ресурсів, визначення оптимальних запасів (нафтопродуктів, запасних частин тощо).

Методи динамічного програмування використовують для обґрунту­вання рішень у багатоетапних процесах. При цьому здійснюється зна­ходження кращого рішення на кожному етапі (кроці), яке забезпечувало б оптимальний сукупний результат, тобто за сумою всіх кроків.

До задач такого класу можна віднести розподіл ресурсів у часі, коли кроками будуть окремі закінчені технологічні цикли.

При вирішенні багатьох інженерних задач необхідно враховувати ці- лочисельні фактори. Так, трактори, сільгоспмашини, обслуговуючий пер­сонал не можна виразити дробовими величинами. У таких випадках ви­користовують цілочисельне програмування, яке об’єднує специфічну групу методів лінійного і динамічного програмувань.

При врахуванні випадкових факторів застосовують імовірнісні методи обгрунтування рішень. Зокрема, цілий ряд інженерних задач можна ви­рішити методами теорії масового обслуговування, яка є складовою части­ною теорії ймовірностей.

Пункти технічного обслуговування, станції заправки паливом, тран­спортно-технологічні процеси можна змоделювати як системи масового обслуговування (СМО). Метою оптимізації СМО є максимізація про­пускної здатності або мінімізація простоїв замовлень при очікуванні об­слуговування.

У сільськогосподарському виробництві нерідко виникають задачі, коли складно врахувати ймовірність появи тих чи інших ситуацій (напри­клад, поведінка конкуруючої сторони). Прийняття рішень в умовах неви­значеності здійснюється з використанням методів теорії статистичних рішень і теорії'ігор. їх метою є зниження величини ризику, обґрунтування такої стратегії поведінки, яка передбачала б певні дії при виникненні тієї чи іншої ситуації.

Багатокритеріальні моделі прийняття рішень враховують декілька цілей. Продуктивність, якість, експлуатаційні затрати, екологічність — ці та інші показники повинні враховуватись при проектуванні виробничих процесів, обгрунтуванні комплексів машин, виборі проекту виробничих об’єктів тощо.

Якщо вдається побудувати узагальнений критерій, який включав би основні часткові критерії, то задача зводиться до багатомірної оптимі­зації. В інших випадках застосовують методи субоптимізації (часткової оптимізації), послідовного використання критеріїв, вибору раціонального рішення за критерієм відстані до цілі.

Методи вибору раціональних рішень переважно є простішими від оптимізаційних і на даний час переважають в інженерній практиці. Вибір раціонального рішення передбачає наявність альтернативних варіантів, критеріїв вибору і правила вирішення.

Із сукупності методів вибору рішень доцільно виділити функці­онально-вартісний аналіз (ФВА), який дозволяє обґрунтувати раціо­нальне рішення за критеріями корисності і плати за корисність (кошти, енергія, шкідливі наслідки). Більшість задач машиновикористання можна вирішити з використанням ФВА. Це пояснюється тим, що на певних етапах даного методу можуть бути використані всі інші методи і процедури. Тобто ФВА практично виступає в ролі технології обґрун­тування рішень.

Евристичні методи прийняття рішень також мають низку ефективних, перевірених практикою процедур. Особливе місце серед них займають ¹ методи колективних рішень, побудова і аналіз карти втрат, методи «за — проти» і «розумовий штурм» тощо.

Розвиток евристичних методів у напрямку алгоритмізації творчого про­цесу суттєво підвищує їх ефективність. Про це свідчить досвід застосування алгоритмів вирішення винахідницьких задач для вдосконалення технічних систем і процесів. Виявлення технічних суперечностей і застосування при­йомів їх усунення, аналіз ресурсів простору і часу, речовини і фізичних полів можуть бути використані для вирішення винахідницьких задач.

Сукупність евристичних і аналітичних методів, процедур і прийомів обґрунтування рішень складає основу інструментарію фахівців інженерної служби, дозволяє підвищити ефективність механізованого виробництва, уникнути грубих прорахунків і нераціональних рішень.