Линейное программирование. Общие задачи оптимизации.
Когда существует несколько вариантов и необходимо выбрать наилучший или наихудший данная задача называется оптимизацией. Математически это сводиться к нахождению минимума или максимума некоторой функции.
f (x) 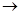 max (min), где x
max (min), где x 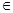 X
X
Определенная таким образом задача называется задачей оптимизации, где
Х – допустимое множество данной задачи
f(x) – целевая функция
в подавляющем большинстве случаев точке х задается несколькими числами
х 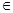 (х1, х2, …, хn), т.е. является точкой n-мерного арифметического пространства (Rn), соответственно Х – это подмножество в Rn, очень много зависит от того как задается множество Х.
(х1, х2, …, хn), т.е. является точкой n-мерного арифметического пространства (Rn), соответственно Х – это подмножество в Rn, очень много зависит от того как задается множество Х.
в большинстве случаев Х выделяется из Rn с помощью системы неравенств.
(2) 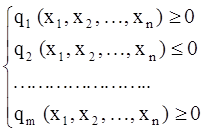
q1, q2 , …, qm – заданные функции в Rn
Х – множество точек х1, х2, …, хn, которые принадлежат Rn и удовлетворяют системе неравенств (2).
В этом случае задача оптимизации приобретает следующий вид: дана функция из n переменных f(x) и система неравенств (2). Требуется найти максимум или минимум f(x) при условиях (2). Надо найти не только само значение максимума или минимума функции, но и точку или точки, если их несколько, в которых это значение достигается, такие точки называются оптимальными решениями. Множество всех оптимальных решений называется оптимальным множеством и обозначается Х*.
Данные задачи являются задачами математического программирования. При этом f(x) – целевая функция, а неравенства из системы (2) – ограничения. В большинстве случаев в эти ограничения входят условия неотрицательности самих переменных (тривиальные ограничения). В зависимости от вида функции f(x), а также функций q1, q2 , …, qm различают разные виды математического программирования.
Когда функции линейные говорят о задаче линейного программирования.

Задачи линейного программирования
№1 Задача о банке.
Собственные средства банка в сумме с депозитами составляет 100 млн. $, часть этих средств, но не менее 35 млн.$ должна быть размещена в кредитах.
Кредиты – не ликвидные активы банка, поэтому существует правило, согласно которому банки должны покупать в определенной пропорции ликвидные активы (ценные бумаги), чтобы компенсировать не ликвидность кредитов.
Ликвидное ограничение: ценные бумаги должны составлять не менее 30 % средств размещенных в кредитах и ценных бумагах в сумме.
c1 – доходность кредита
c2 – доходность ценных бумаг
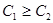
Цель банка: максимизация прибыли.
х1 – средства, размещенные в кредитах
х2 – средства, размещенные в ценных бумагах
f(x) = c1x1 + c2x2 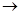 max
max
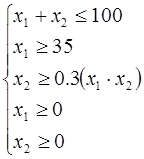
№2 Задача о диете
Из имеющихся продуктов требуется составить диету, которая с одной стороны удовлетворяла бы минимальные потребности организма в питательных веществах, а с другой стороны требовала наименьших затрат
| A | B | C | Цена | |
| В 1 кг П1 | a1 | b1 | c1 | S1 |
| В 1 кг П2 | a2 | b2 | c2 | S2 |
| Потребность | a | b | c |
х1 – оптимальное количество продукта 1 (кг)
х2 – оптимальное количество продукта 2 (кг)
f(x) = s1x1 + s2x2 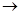 min
min
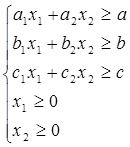
К подобной задаче могут быть сведены задачи определения состава сплавов, смесей, горючего, кормов, минеральных удобрений.
№3 Задача об использовании ресурсов
Предприятие имеет в своем распоряжении определенное количество ресурсов
| Товары Ресурсы | T1 | T2 | Количество ресурса |
| R1 | a11 | a12 | b1 |
| R2 | a21 | a22 | b2 |
| R3 | a31 | a32 | b3 |
| Доход от 1 ед. | c1 | c2 |
х1 – оптимальное количество товара 1 (кг)
х2 – оптимальное количество товара 2 (кг)
f(x) = c1x1 + c2x2 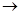 max
max
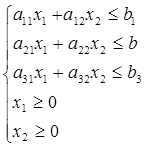
№4 Транспортная задача
Уголь, добываемый в нескольких месторождениях, отправляется потребителям известно, сколько угля добывается в каждом из месторождений и сколько его требуется любому из потребителей, известно, сколько стоит перевозки 1 ед. угля. Требуется спланировать перевозки угля, т.о. чтобы затраты на перевозку были минимальны.
| Потребители Пост-ки | П1 | П2 | П3 | Количество угля |
| М1 | c11\x1 | c12\x2 | c13\x3 | a1 |
| М2 | c21 \x4 | c22\x5 | c23\x6 | a2 |
| Потребности | b1 | b2 | b3 |
х1-6 – оптимальное количество перевозимого угля
Транспортная задача является открытой, если a1 + a2 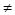 b1 + b2 + b3.
b1 + b2 + b3.
Транспортная задача закрытого типа a1 + a2 = b1 + b2 + b3.
f(x) = c11*x1 + c12*x2 + c13*x3 + c21 *x4 + c22*x5 + c23*x6  min
min
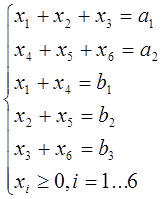
Дата добавления: 2015-05-13; просмотров: 858;
