Круг равных высот (КРВ)
Зенит для такого наблюдателя будет находиться в точке Zc, которая находится на небесном меридиане светила, а 
Zcσ есть зенитное расстояние
| Zc = 90° − hc |
То есть, высота светила для наблюдателя, находящегося на поверхности Земли в точке «c» уже не будет равна 90°00,0′, а будет иметь какое-то другое, вполне определенное значение hc.
Отложив по меридиану полюса освещения отрезок дуги ab = ac, убеждаемся, что наблюдатель, находящийся на поверхности Земли в точке b, будет наблюдать светило σ на такой же высоте (hb = hc), что и наблюдатель, находящийся на поверхности Земли в точке «c», так как зенитное расстояние Zcσ равно зенитному расстоянию Zbσ по построению.
Если провести на поверхности Земли окружность сферическим радиусом R = ab = ac с центром в полюсе освещения (в точке а), то окажется, что в какой бы точке этой окружности ни находился наблюдатель, он будет видеть светило σ на одной и той же высоте hc = 90°– Z (в один и тот же момент времени).
Малый круг на поверхности Земли, в любой точке которого определенное светило имеет в данный конкретный момент времени одну и ту же высоту, называется кругом равных высот (КРВ).
Круг равных высот является астрономической изолинией положения наблюдателя на поверхности Земли. Если h* = 90°, то КРВ представляет собой точку - полюс освещения светила. Чем меньше высота светила, тем больший радиус будет иметь КРВ.
Если h* = 0, то наблюдатель видит светило на самой линии горизонта и КРВ становится большим кругом, разделяющим поверхность Земли на освещенную и неосвещенную одинаковые части.
Такой большой круг называется кругом освещения.
Каждому КРВ на поверхности Земли соответствует свой круг на небесной сфере с центром в видимом месте светила (σ) и сферическим радиусом, равным зенитному расстоянию светила, то есть
| R = Z = 90° − hc |
Этот круг на небесной сфере называют кругом равных зенитных расстояний (КРЗР) и он является астрономической изолинией положения зенита наблюдателя на небесной сфере.
Круги равных высот нетрудно нанести на глобус.
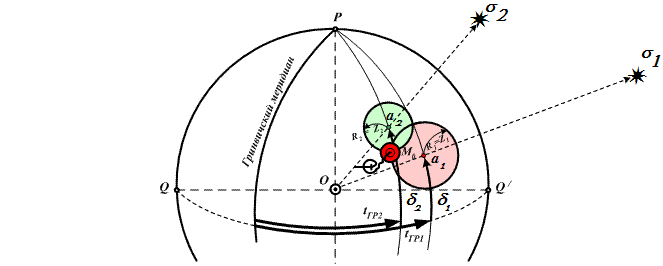
Допустим, что в какой-то момент времени (Т) одновременно измерены высоты двух светил, рассчитаны истинные значения этих высот (h1 и h2) и определены значения зенитных расстояний:
Z1 = 90° − h1 Z2 = 90° − h2
По значению гринвичского времени замера высот, из МАЕ выбраны значения экваториальных координат (δ и tГР) этих светил.
По значениям экваториальных координат светил на глобусе Земли найдены их полюсы освещения: точкаa1 → по δ1 = φ1 и tГР1 = λ1; точка a2 → по δ2 = φ2 и tГР2 = λ2 .
Дата добавления: 2015-05-13; просмотров: 2207;