Лекция 16. Автокорреляция и ее вычисление
|
Пусть задана бесконечная последовательность 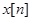 . По ней строится автокорреляционная функция
. По ней строится автокорреляционная функция 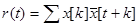 . Эта функция играет огромное значение в при обработке сигналов. Основное назначение - отыскание максимумов функции
. Эта функция играет огромное значение в при обработке сигналов. Основное назначение - отыскание максимумов функции 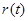 , которые интерпретируются как аналоги периодов. Из неравенства Коши следует, что
, которые интерпретируются как аналоги периодов. Из неравенства Коши следует, что 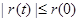 . В точках максимума
. В точках максимума 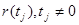 сдвинутая на
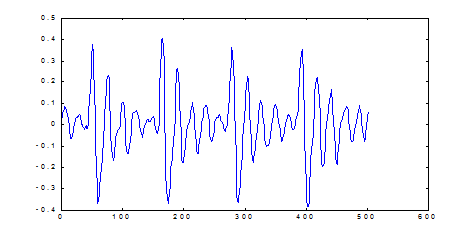
сдвинутая на 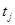 исходная последовательность "похожа" на исходную. В качестве примера рассмотрим фрагмент звукового файла с записью звука "а". Этот сигнал не является периодическим в математическом смысле слова, однако, визуально такая периодичность просматривается. Значения периода находятся по максимумам соответствующей автокорреляционной функции. Найдем преобразование Фурье от
исходная последовательность "похожа" на исходную. В качестве примера рассмотрим фрагмент звукового файла с записью звука "а". Этот сигнал не является периодическим в математическом смысле слова, однако, визуально такая периодичность просматривается. Значения периода находятся по максимумам соответствующей автокорреляционной функции. Найдем преобразование Фурье от 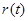 . Для непрерывного случая эта задача рассматривалась выше. Положим
. Для непрерывного случая эта задача рассматривалась выше. Положим 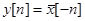 . Теперь
. Теперь 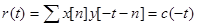 , где
, где 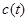 - свертка последовательностей.
- свертка последовательностей. 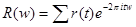 =
= 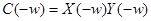 . С другой стороны,
. С другой стороны, 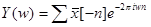 =
= 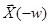 . Это означает, что
. Это означает, что 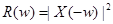 . Если исходная последовательность вещественная, то
. Если исходная последовательность вещественная, то 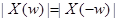 и
и
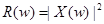 (1)
(1)
Дата добавления: 2015-05-13; просмотров: 912;
