Параметры систем

Сложность структуры системы опреде­ляется числом п ее элементов и числом т связей между ними. Если в какой-либо системе исследуется число частных дискретных состояний, то сложность системы С определя­ется логарифмом числа связей:

C = lg m. (1)

Системы условно классифицируются по сложности следующим образом:

1) системы, имеющие до тысячи состояний (О <С < 3), относятся к простым,

2) системы, имеющие до миллиона состояний (3 < С < 6), являют собой сложные системы,

3) системы с числом состояний свыше миллиона (С > 6) идентифицируются как очень сложные.

Все реальные природные биосистемы очень сложны. Даже в структуре единичного вируса число биологически значимых моле­кулярных состояний превышает последнее значение. Кроме того, существует и другой критерий сложности, связанный с поведением системы, ее реакцией на внешнее воздействие. Если система способ­на к акту решения, т.е. к выбору альтернатив поведения (в том числе и с помощью случайного механизма), то такая решающая система считается сложной. Сложной будет и любая система, включающая в себя в качестве подсистемы хотя бы одну решающую систему.

2. Разнообразие состава или взаимосвязей в системе оценивается показателем Е. Симпсона

D_s = 1 -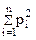

или показателем К. Шеннона

H_s = –

где D_s, H_s — индексы разнообразия;

p_i — относительная численность (частота встречаемости) i-й разно­видности элементов в совокупности п разновидностей ( 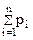= 1).

Эти показатели важны при количественной оценке биоразнооб­разия экосистем и принципиально отличаются от числа представ­ленных в экосистеме видов.

Например, пусть существуют два одинаковых по суммарной чис­ленности (100) набора состава древостоя: А — сосна (35), береза (35), ель (30); Б — сосна (90), береза (3), ель (2), осина (2), пихта (1), дуб (1), клен (1). Рассчитанные в соответствии с показателями Симпсона (2.2) индексы разнообразия равны соответственно D_A = 0,665 и D_Б = 0,188. Те же индексы, рассчитанные по Шеннону, т.е. по формуле (2.3), соответственно равны H_A = 0,548 и H_Б =0,216. Хотя в составе Б вдвое больше видов, но собственно разнообразие в 2,5—3,5 раза меньше, так как это типичный сосняк с малой примесью других видов, тогда как состав А — типичный смешанный лес.

3. Вычисление разнообразия по формуле К. Шеннона — это ча­стный случай расчета количества информации для оценки неопреде­ленности функционирования системы:

H = –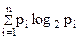

где p_i — вероятность реализации i-того события;

-log₂ p_i — количество информации, соответствующее i-му событию.

Это выражение приводит к интерпретации такого физического по­нятия, как энтропия, — важного параметра состояния любой динами­ческой системы. В аналогичном вероятностно-информационном оп­ределении энтропии S символ p_i обозначает вероятность того, что система находится в некотором i-м состоянии:

где k_Б - постоянная Больцмана, равная 1,3807 • 10^-23 Дж/град.

Энтропия как мера необратимого рассеяния (диссипации) энер­гии при ее превращениях и вероятность пребывания системы в данном термодинамическом состоянии (принцип Л. Больцмана) выступает здесь и как мера вероятностной неупорядоченности, хао-тизации элементов системы (Волькенштейн, 1984).

4. При условии, что для каждого элемента системы возможны два состояния (основное и возбужденное) и они равновероятны (в этом случае -log₂ p_i = 1 бит информации), отношение I_S= H/S мо­жет служить в качестве информационного эквивалента энтропии: I_S = 4,38 • 10²³ бит на одну энтропийную единицу или 1,045 • 10²³ бит наДж/К¹.

Поскольку

∆S = ∆Q/T,

где Q — количество теплоты (энергии);

Т — абсолютная температура, знание которой позволяет оценить ин­формационный эквивалент энергии:

I_Е = 1,045 • 10²³ 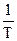бит/Дж.

Это означает, что в энергетическом отношении структурная информация сама по себе чрезвычайно «дешева». Ее обратная зави­симость от температуры имеет скрытое универсальное значение и представляет самостоятельный интерес.

Сама по себе энтропия и тем самым неопределенность состоя­ния системы может только возрастать, т.е. информация сама по се­бе может только утрачиваться. Только в открытых системах (с на­качкой), отдающих энтропию, информация может приобретаться. Поэтому переработку информации можно рассматривать как некую частную разновидность самоорганизации.

5. Оценка относительной организации системы R, зависящая от сложности и разнообразия состава, рассчитывается по формуле:

R= 1 –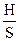

По этому параметру системы также разделяются на три группы:

1) если оценка R мала (0 < R < 0,1), то система считается веро­ятностной, неустойчивой, обладающей малой жесткостью и спо­собной гибко изменять свои состояния;

2) если значение R сравнительно велико (0,3 < R <1), то систе­ма считается детерминированной, т.е. консервативной, жесткой, ус­тойчивой;

3) промежуточное положение занимают квазидетерминированные системы (0,1 <R < 0,3).

Большинство природных биосистем имеет вероятностный или квазидетерминированный характер.

Организмы обладают иерархией структур и функций, в которой по мере усложнения организации возрастает разнообразие системных качеств. В ходе их эволюции образуются и приобретают все большее значение выделенные структуры управления. В отличие от них при­родные вероятностные системы, состоящие из большого числа слабо скоррелированных индивидуумов (экосистемы), могут обладать функциональной иерархией особей, но не нуждаются в выделенной внутренней системе управления. Они способны к самоподдержанию и во многих случаях без каких бы то ни было «центральных регуля­торов» обнаруживают удивительно тонкую и точную авторегуляцию.