Анализ конструкций центробежных насосов

Генетические алгоритмы (ГА) (genetic algorithms) – большая группа методов адаптивного поиска и многопараметрической оптимизации, связанная принципами естественного отбора и генетики.

В общем случае при использовании ГА задачи оптимизации имеют следующую математическую формулировку:

найти такое значения варьируемых параметров 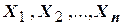, которые минимизируют целевую функцию 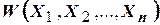при условии, что указанные параметры 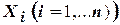удовлетворяют допустимой области 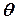, задание которой диктуется спецификой решаемой задачи.

В качестве варьируемых параметров в этих случаях могут быть числовые коэффициенты регрессионной модели; число базисных функций; порядок уравнений регрессии; числовые коэффициенты 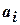, , 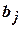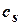функций принадлежности; число функций принадлежности; число слоев и число нейронов в каждом слое нейронной сети.

При указанных варьируемых параметрах целевыми функциями могут быть: ошибка идентификации и прогноза в текущий или будущий момент времени; один из показателей качества процесса (функционал); ошибка обучения НС – рассогласование между выходными объекта и эталонной модели системы.

Наиболее общее определение: генетические алгоритмы (ГА) – это методы случайного глобального поиска, копирующие механизмы естественной биологической эволюции.

Следует отметить, что существует много различных модификаций ГА. Здесь рассмотрим элементы простейшего его варианта – стандартного.

Стандартный ГА – метод стохастической оптимизации для задач дискретной оптимизации вида.

Здесь 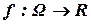– функция пригодности (fitness function); 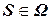– 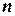-мерный двоичный вектор из дискретного множества 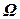– хромосома (chromosome) или двоичная нить (string) длины 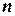. Множество 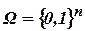– множество вершин 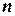- мерного гиперкуба с единичным ребром; 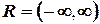– множество действительных чисел.

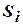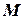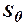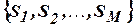
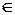
Главное отличие стандартного ГА от традиционных методов оптимизации – на каждом шаге ГА имеет дело сразу с несколькими значениями вектора параметров , которые образуют популяцию (population) хромосом. В начале процедуры поиска создается начальная популяция, например, из двоичных хромосом: = 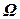, каждая из которых содержит 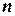битов. Такая популяция создается либо случайным образом, либо с учетом априорной информации об области нахождения оптимума в множестве .

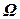Под двоичным вектором-хромосомой 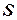понимается двоичное кодирование исходного варьируемого параметра 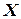, физический смысл которого определяется задачей. Длина хромосомы 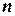(число битов) при таком кодировании зависит от требуемой точности нахождения оптимума параметра 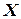и должна удовлетворять условию

,

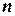
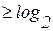
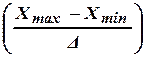где 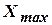, 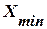– предельные значения параметра 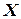; 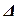– заданная погрешность определения его оптимального значения.

Число членов 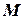в популяции влияет на широту фронта поиска и задается эмпирически.

Вычисление последующих популяций 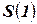, 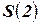и т.д. на базе 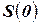осуществляется путем применения трех генетических операторов: отбора (selection), кроссинговера (crossingover) и мутации (mutation).

Отбор в стандартном ГА реализуется методом «колеса рулетки», при котором хромосомы-кандидаты из 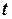-го поколения 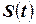выбираются для выживания в следующем, 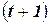-м поколении 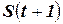путем использования колеса рулетки. Каждая хромосома в популяции представлена на колесе в виде сектора с шириной, пропорциональной функции пригодности 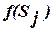. Для отбора 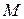хромосом колесо рулетки вращают 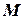раз. В результате по завершении каждого вращения выделяется одна из хромосом 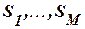, которые принимаются в качестве кандидатов в следующем поколении. Перед их копированием в новую популяцию они должны подвергнуться кроссинговеру и мутации.

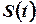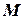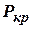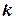
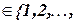
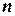
Оператор кроссинговера (скрещивания) применяется к паре хромосом из (пусть -четное), прошедших отбор. – назначаемая вероятность выполнения кроссинговера. Далее для случайно выбранной пары хромосом определяется случайное число 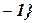(место или сайт кроссинговера), и затем биты из двух выбранных хромосом меняются местами после 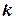-го бита с вероятностью 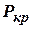. Процесс повторяется до момента, когда популяция 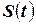не окажется пустой.

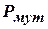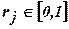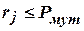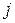Оператор мутации состоит в случайном изменении (на противоположное) значения каждого бита гена с вероятностью . Самым легким способом определения изменяемых бит (если это необходимо) – выбор независимого случайного числа для каждого бита хромосомы. Если , то -й бит следует изменить, в противном случае он сохраняется.

После мутации хромосомы-кандидаты копируются в новую популяцию хромосом 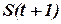и весь процесс повторяется с вычислением функции пригодности для каждой хромосомы и применением операторов отбора, кроссинговера и мутации (рис. 5.8.) [4].

Отбор методом «колеса рулетки» позволяет претендовать на выживание хромосомам с пригодностью выше среднего. Детерминированный подход по принципу выбора хромосом с наибольшей пригодностью не применяется в соответствии с допущениями генетического поиска, согласно которым даже хромосомы с низкой пригодностью могут содержать полезную инфор­мацию.

Наиболее критическим из перечисленных трех является оператор кроссинговера, так как он отвечает за смешивание информации хромосом поколение попу­ляции, а от этого зависит глобальность получаемых резу­льтатов. Установлено эмпири­чески, что .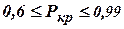

Операторы отбора и кроссинговера используются для улучшения структуры хромосом. Цель оператора мутации – диверсификация, т.е. повышение разнообразия поиска и введение новых хромосом в популяцию для большей полноты исследования пространства поиска. Мутация инициирует разнообразие в популяции, позволяя просматривать больше точек в пространстве поиска и преодолевать локальные эксперименты в ходе поиска. Частое применение мутации приводит к разрушению хромосом с высокой приспособленностью в популяции, что сказывается на сходимости решения. Поэтому применение мутации обычно осуществляется с малой вероятностью: .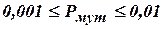

В последнее время область применения ГА значительно расширилась. Данные методы оказываются эффективными при решении следующих задач :

· идентификация сложных динамических объектов;

· выбор оптимальной конфигурации многоагентных робототехнических систем;

· синтез оптимальных алгоритмов управления многозвенными роботами-манипуляторами;

· оптимальное управление стыковкой космических аппаратов;

· планирование маршрутов движения транспортных средств в условиях препятствий;

· структурный синтез проектных решений, синтез расписаний

и многих других.

Таким образом, применение ГА охватывает не только класс традиционных задач оптимизации, но и быстро распространяется на задачи управления сложными динамическими объектами в условиях неопределенности. Нельзя не отметить, что область применения ГА существенно расширилась. Одним из таких расширений является генетическое программирование (ГП), под которым понимается применение генетической модели обучения в пространстве программ. В этом случае в качестве индивидуумов, составляющих популяцию, выступают уже не указанные выше достаточно простые линейные структуры – хромосомы, а компьютерные программы, которые, будучи исполненными, представляют собой кандидатов на решение поставленной задачи.

Анализ конструкций центробежных насосов