Уравнение теплового баланса ЭП
При работе ЭД в различных условиях и при различных нагрузках на его валу изменяются условия протекания тепловых процессов ЭД. Как известно работа ЭД сопровождается потерями мощности 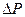 , которые складываются из магнитных потерь (в стали), электрических потерь (потерь в меди), а также механических потерь. За время
, которые складываются из магнитных потерь (в стали), электрических потерь (потерь в меди), а также механических потерь. За время  двигатель с потерями мощности равными
двигатель с потерями мощности равными 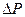 выделяет количество тепла равное
выделяет количество тепла равное 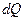 . Это тепло во-первых расходуется на нагревание самого двигателя, а во вторых рассеивается в окружающую среду:
. Это тепло во-первых расходуется на нагревание самого двигателя, а во вторых рассеивается в окружающую среду:
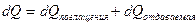 (99)
(99)
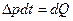 (100)
(100)
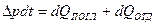 (101)
(101)
В начале основная часть выделяемого тепла идет на нагревание самого двигателя и значительно меньшая часть отдается в окружающую среду. В процессе нагревания ЭД это соотношение изменяется в сторону 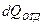 и при некоторой температуре двигателя наступает установившийся режим, после чего всё выделяемое при работе тепло рассеивается в окружающую среду, а температура двигателя при условии неизменности нагрузки на его валу в дальнейшем не меняется. Необходимо отметить, что реальные термодинамические процессы в ЭП носят весьма сложный характер, т.к. электрические машины во первых не однородна по материалу, во вторых имеет рассредоточенные внутренние источники тепла, интенсивность которых зависит от режима, скорости и т.д. Поэтому для дальнейшего анализа тепловых переходных процессов в ЭП, применим следующие допущения:
и при некоторой температуре двигателя наступает установившийся режим, после чего всё выделяемое при работе тепло рассеивается в окружающую среду, а температура двигателя при условии неизменности нагрузки на его валу в дальнейшем не меняется. Необходимо отметить, что реальные термодинамические процессы в ЭП носят весьма сложный характер, т.к. электрические машины во первых не однородна по материалу, во вторых имеет рассредоточенные внутренние источники тепла, интенсивность которых зависит от режима, скорости и т.д. Поэтому для дальнейшего анализа тепловых переходных процессов в ЭП, применим следующие допущения:
1. Электрическая машина является однородным телом с одинаковой по всему телу теплоёмкостью 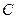 и с одинаковой температурой по всем точкам объема тела.
и с одинаковой температурой по всем точкам объема тела.
2. Теплоотдача в окружающую среду пропорциональна разности температур двигателя и окружающей среды, т.е.:
 (102)
(102)
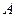 - теплоотдача
- теплоотдача
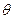 - температура двигателя в градусах
- температура двигателя в градусах
 - температура окружающей среды
- температура окружающей среды
Чаще всего при анализе тепловых переходных процессов в качестве  применяется ее нормативное значение
применяется ее нормативное значение 
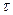 - превышение температуры
- превышение температуры  двигателя или еще один термин: температура перегрева.
двигателя или еще один термин: температура перегрева.

С учетом этих допущений, уравнение (3) запишется в виде:
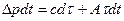 (103)
(103)
где 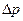 -потери мощности в двигателе
-потери мощности в двигателе
 -промежуток времени (длительность переходного процесса)
-промежуток времени (длительность переходного процесса)
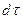 -изменение превышения температуры
-изменение превышения температуры
Теплоёмкость – численно равна количеству тепла, необходимое для нагрева двигателя на 1 градус.
Теплоотдача – количеству тепла, выделявшему в ОС при изменении температуры на один градус за время равное 1 секунде.
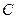 -пропорциональна кубу габаритов.
-пропорциональна кубу габаритов.
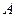 -пропорциональна квадрату габаритов.
-пропорциональна квадрату габаритов.
Если разделить все члены уравнения (103) на  , то
, то
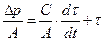 (104)
(104)
Уравнение (104) описывает тепловые переходные процессы в ЭД и в частном случае для установившегося режима примет вид:
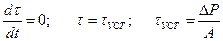
Если в уравнении (104) отношение 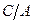 (сек) обозначим
(сек) обозначим 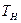 - постоянна времени нагрева,то с учётом этого уравнение (104) будет иметь вид:
- постоянна времени нагрева,то с учётом этого уравнение (104) будет иметь вид:
 (105)
(105)
Уравнение (105) представляет собой дифференциальное уравнение 1-го порядка и носит название дифференциальное уравнение теплового баланса. При нагреве от некоторого начального значения 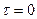 до
до 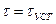 . Решение этого уравнения имеет вид:
. Решение этого уравнения имеет вид:
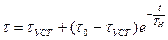
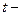 текущее время (с).
текущее время (с).
Графически это уравнение может быть представлено в виде экспоненциальной функции следующего вида:
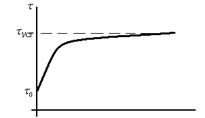
Рис.79а Кривая нагрева при τ0=0
В частном случае если включение двигателя происходит в момент, когда его температура равна температуре окружающей среды, график будет иметь следующий вид:

Рис. 79б Кривая нагрева при τ0=0
Если двигатель в процессе работы нагреть до 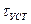 , а затем выключить из питающей сети, то процесс его охлаждения до температуры окружающей среды может быть представлен в виде уравнения, которое носит название решение уравнения теплового баланса при охлаждении и имеет следующий вид:
, а затем выключить из питающей сети, то процесс его охлаждения до температуры окружающей среды может быть представлен в виде уравнения, которое носит название решение уравнения теплового баланса при охлаждении и имеет следующий вид:
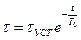 (106)
(106)
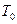 - постоянная времени охлаждения она имеет такой же физический смысл что и постоянная времени нагрева, но в силу того, что в термодинамике процессы охлаждения имеют несколько большую инерционность, чем процессы нагрева для одного и того же двигателя, находятся примерно в таком соотношении:
- постоянная времени охлаждения она имеет такой же физический смысл что и постоянная времени нагрева, но в силу того, что в термодинамике процессы охлаждения имеют несколько большую инерционность, чем процессы нагрева для одного и того же двигателя, находятся примерно в таком соотношении:
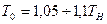
Дата добавления: 2015-05-08; просмотров: 1081;
