Кодирование чисел

Кодирование знака числа. Кодирование чисел позволяет заменить операцию арифметического вычитания операцией алгебраического сложения с помощью двоичного сумматора. Для кодирования знака числа используется специальный двоичный разряд, называемый знаковым. При этом знак плюс кодируется двоичной цифрой 0, а минус – цифрой 1 (для системы счисления с основанием r – цифрой r-1). Для машинного представления отрицательных чисел используют три основных вида кодов: прямой, обратный и дополнительный. Общая схема кода числа: код знака . код числа.

Прямой код числа. При этом способе кодирования чисел кодируется только знак числа, а значащая часть остается без изменения.

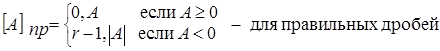
Пример: A=+0,1101 A=+ 1101

[A]_пр=0,1101 [A]_пр=0.1101

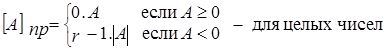
Пример: A = - 0,1101 A = - 1101

[A]_пр=1,1101 [A]_пр=1.1101

Диапазон изменения машинных изображений для прямого кода лежит в пределах: -(1-2^-n) [A]_пр (1-2^-n).

Недостатком прямого кода является сложность выполнения операции сложения чисел с разными знаками.

Для арифметических операций над числами в прямом коде используется сумматор прямого кода. В этом сумматоре отсутствует цепь поразрядного переноса между старшим значащим и знаковым разрядами, то есть на этом сумматоре невозможно выполнение операции алгебраического сложения.

Дополнительный код числа. Число А¢ называется дополнением к числу А, если выполняется соотношение: А + А¢ = rⁿ для целых чисел, или А + А^'=r⁰ для дробных чисел, где n- количество цифр в записи числа A.

Пример: A₁₀ =378

n=3

A₁₀¢ =10³ – А₁₀=1000 - 378=622

621 - все разряды дополняются до младшей цифры системы счисления

1 - младший разряд дополняется до основания системы счисления

n=4

А₂ =1011, 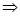A₂ ¢=2⁴ - А=10000 - 1011 = 0101 или А₂¢ = 0101

Замена операции вычитания операцией сложения. В ЭВМ достаточно сложно выполнить операцию вычитания (А-В). Для этого требуется:

1) сравнить числа и выявить наибольшее по абсолютной величине;

2) наибольшее число разместить на входах вычитающего устройства;

3) выполнить операцию вычитания;

4) присвоить знак разности наибольшего по величине числа.

Для сложения чисел требуется сумматор и неважно, какие слагаемые подаются на его входы А или В. Пусть необходимо сложить

А = 487 А = 487

В = -348 В = 652

А-В = 139 А-В = 1 139

А + (10³ – В) = А-В+10³ (10³ игнорируется).

А = 348 А = 348

В = -487 В = 513

А-В = -139 А-В = 861

Дополнительный код является математическим дополнением основания системы счисления.

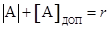- для дробных чисел, 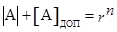- для целых чисел

где 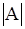- абсолютное значение числа А, n – число цифр числа.

Положительные числа в дополнительном коде не меняют своего изображения. Правило преобразования числа в дополнительный код можно записать:

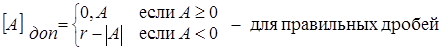
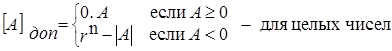
Рассмотрим несколько примеров сложения чисел в дополнительных кодах.

А= 0,1001 [A]_доп = 0,1001 А= - 0,1001 [A]_доп = 1,0111

В= - 0,0100 [B]_доп = 1,1100 В= 0,0100 [B]_доп = 0,0100

10,0101 1,1011

Теорема. Сумма дополнительных кодов чисел есть дополнительный код результата.

Доказательство теоремы приведено в [1].

Теорема справедлива для всех случаев, в которых не возникает переполнения разрядной сетки, что позволяет складывать машинные представления чисел по правилам двоичной арифметики, не разделяя знаковую и значащую части числа. Для выполнения арифметических операций над числами в дополнительном коде используется двоичный сумматор дополнительного кода, характерной особенностью которого является наличие поразрядного переноса из старшего значащего в знаковый разряд.

Обратный код числа. Обратный код двоичного числа является инверсным изображением числа, в котором все разряды исходного числа принимают инверсное (обратное) значение. Правила преобразования чисел в обратный код аналитически можно определить следующим образом:

,

.

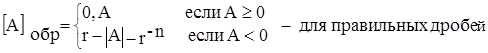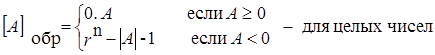Выполнение арифметических операций над числами в обратном коде осуществляется на сумматоре обратного кода. Этот код имеет несущественный недостаток: требует наличия в сумматоре цепи циклического переноса из знакового разряда в младший значащий. Это может привести к увеличению времени выполнения арифметических операций. Ниже приведены несколько примеров выполнения арифметических операций над числами, записанными в дополнительном коде.

А= 0,1001 [A]_обр = 0,1001 А= - 0,1001 [A]_обр = 1,0110

В= - 0,0100 [B]_обр = 1,1011 В= 0,0100 [B]_обр = 0,0100

10,0100 1,1010

1

0,0101

Теорема. Сумма обратных кодов чисел есть обратный код результата.

Доказательство теоремы приведено в [1].