Перевод целых чисел.
Метод подбора степеней основания. В соответствии с (2) целые числа в системах счисления с основаниями r1 и r2 могут быть представлены:
n k
A r1 = 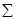 ai r1i =
ai r1i = 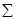 bj r2j = A r2 ,
bj r2j = A r2 ,
i=0 j=0
В общем случае перевод числа из системы счисления с основанием r1 в систему счисления с основанием r2 можно представить как задачу определения коэффициентов bi нового ряда, изображающего число в системе счисления с основанием r2. Основная трудность в выборе максимальной степени основания r2, которая еще содержится в числе Ar1. Все действия должны выполняться по правилам r1-арифметики (то есть исходной системы счисления). После нахождения максимальной степени и соответствующего ей коэффициента необходимо найти коэффициенты для всех остальных (младших) степеней.
Пример: A10=37 , A2=?
37=1·25 + 0 ·24 + 0 ·23 + 1·22 + 0 ·21 + 1·20=100101
Нечетным двоичным числом 100101 является число, содержащее единицу в младшем разряде.
Метод деления на основание системы счисления. На основании (1) число Ar1 в системе счисления с основанием r2 запишется в виде:
Ar2 = an· r2n + an-1 ·r2n-1 + ... + a1· r21 + a0·r0.
Переписав это выражение по схеме Горнера, получим:
Ar2 = (...(an r2 + an-1) r2 + ... + a1) r2 + a0.
Разделив правую часть на r2, получим первый остаток a0 и целую часть
(...(an r2 + an-1) r2 + ... + a1). Разделив целую часть на r2, получим остаток a1 и новую целую часть. Выполнив деление n+1 раз, получим последнее целое частное an < r2, являющееся старшей цифрой числа.
Пример А10 = 37 ; A2 = ?; А5=?
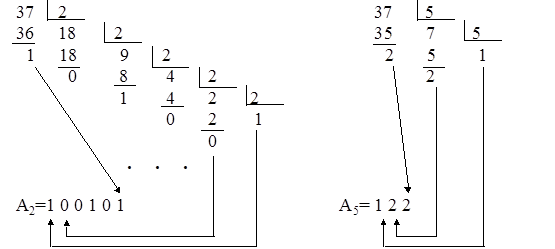
Дата добавления: 2015-05-05; просмотров: 808;
