Определение траектории, скорости и ускорения точки, при движении её в координатной форме.

Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат.

Движение точки в пространстве задается тремя уравнениями:

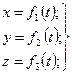(3.1)

Движение точки в плоскости (рис. 17) задается двумя уравнениями:

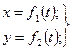(3.2)

Системы уравнений (1) или (2) называют законом движения точки в координатной форме.

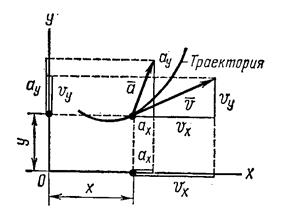
рис.17

Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).

Если закон движения точки задан в координатной форме, то

A). траектория плоского движения точки выражается уравнением

,

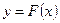которое образуется из данных уравнений движения после исключения времени ;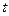

B). числовое значение скорости точки находится из формулы

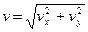
после предварительного определения проекции (см. рис. 17) скорости на оси координат

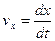и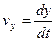

C). числовое значение ускорения находится из формулы

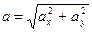
после предварительного определения проекций ускорения на оси координат

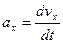и ;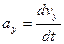

Направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.

Используя уравнения движения точки в координатной форме, можно определить радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу

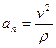
выражающую числовое значение нормального ускорения.

Отсюд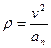а

. (а)

Скорость 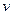точки определяется по формуле

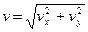. (б)

Следовательно,

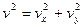. (б’)

Числовое значение нормального ускорения 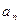входит в выражение полного ускорения точки

,

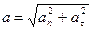откуда

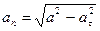, (в)

где квадрат полного ускорения

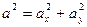(г)

и касательное ускорение

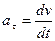. (д)