Цель работы: Экспериментально определить величину дисперсии и коэффициент дисперсии стеклянной призмы; научиться работать со спектроскопом.
Оборудование: спектроскоп твухтрубный, трубка с водородом, катушка Румкорфа, выпрямитель ВС-4-24, РНШ, штатив.
Теория.
Опыт показывает, что коэффициент преломления среды nзависит от 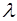 - длины световой волны, т.е. n есть функция от
- длины световой волны, т.е. n есть функция от 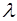
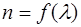 .
.
Само явление зависимости коэффициента преломления n от 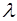 называется дисперсией света, а функция
называется дисперсией света, а функция 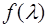 характеризует дисперсионную способность вещества. Следует подчеркнуть, что наличие дисперсии света явилось в свое время одним из фундаментальных затруднений первоначальной электромагнитной теории света Максвелла.
характеризует дисперсионную способность вещества. Следует подчеркнуть, что наличие дисперсии света явилось в свое время одним из фундаментальных затруднений первоначальной электромагнитной теории света Максвелла.
Согласно теории Максвелла скорость света в веществе определяется, как
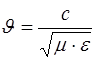 (1)
(1)
С другой стороны абсолютный показатель преломления среды равен:
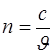 (2)
(2)
Сравнивая выражения (1) и (2) получим, что
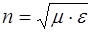 (3)
(3)
Но в теории Максвелла 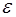 и
и 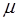 рассматривались как постоянные величины, независимые от
рассматривались как постоянные величины, независимые от 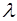 или частоты ν, следовательно, n получилась независимым от
или частоты ν, следовательно, n получилась независимым от 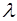 .
.
Таким образом, явление дисперсии, т.е. факт зависимости n от 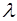 осталось необъяснимым в теории Максвелла.
осталось необъяснимым в теории Максвелла.
Эти затруднения электромагнитной теории Максвелла были устранены электронной теорией Лоренца, которая раскрыла микроскопический смысл макроскопических величин 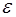 и
и 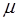 и объяснила их зависимость от
и объяснила их зависимость от 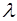 .
.
В 1666 году Ньютон впервые провел экспериментальные исследования дисперсии. Пропустив белый пучок света от щели через призму, преломляющее ребро которой параллельно щели и перпендикулярно плоскости рисунка, и проецируя изображение щели на экран, он получил изображение щели в виде цветной полосы. (рис.1.)

рис.1.
где 1 – источник света, 2 – конденсор, 3 – щель, расположенная перпендикулярно рисунку, 4 – объектив, 5 – призма, преломляющее ребро которой (А) параллельно щели, 6 – экран.
Если сравнивать спектры, полученные с помощью призм с равными преломляющими углами, но из разных веществ, можно заметить, что спектры не только отклонены на разные углы по отношению к белому изображению щели, но и растянуты на большую или меньшую ширину.
Количественной мерой дисперсии служит величина 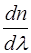 , которая показывает как быстро меняется коэффициент преломления n с изменением
, которая показывает как быстро меняется коэффициент преломления n с изменением 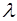
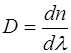
Для исследования дисперсионной способности призмы, т.е. функции 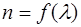 , Ньютон в 1672 г. применил метод скрещенных призм (рис.2.), который показал, что фиолетовые волны преломляются больше, чем красные.
, Ньютон в 1672 г. применил метод скрещенных призм (рис.2.), который показал, что фиолетовые волны преломляются больше, чем красные.
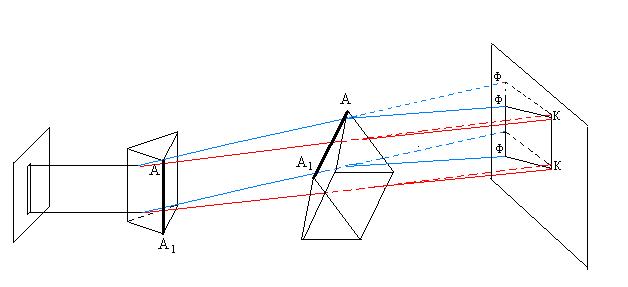
рис.2.
Величина 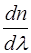 различна в разных областях спектра для одной и той же призмы, максимальна она для фиолетовых лучей (рис.3), поэтому фиолетовая часть спектра более растянута. Различие в величинах дисперсии в разных частях спектра видно из различного наклона касательных к кривой
различна в разных областях спектра для одной и той же призмы, максимальна она для фиолетовых лучей (рис.3), поэтому фиолетовая часть спектра более растянута. Различие в величинах дисперсии в разных частях спектра видно из различного наклона касательных к кривой 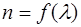 к оси
к оси 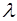 . Из графика на рис.3. видно, что
. Из графика на рис.3. видно, что

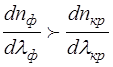
Такую зависимость показатель преломления nимеет для прозрачных тел (стекла, кварца) на всем протяжении видимого спектра (рис.3.) – нормальная дисперсия.
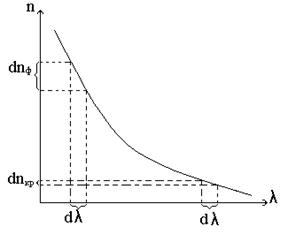 |
рис.3.
В 1862 году Леру наблюдал преломление в призме, наполненной парами йода, в котором при уменьшении длины волны 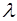 уменьшался и показатель преломления паров йода n. Эту особенность Леру назвал аномальной дисперсией.
уменьшался и показатель преломления паров йода n. Эту особенность Леру назвал аномальной дисперсией.
Систематические исследования Кундта, который использовал для этих наблюдений метод скрещенных призм, позволили установить закон, согласно которому явление аномальной дисперсии тесно связанно с поглощением света: все тела, дающие аномальную дисперсию в какой-либо области, сильно поглощают свет в этой области.
Опыт показывает, что все вещества поглощают свет, в некоторой области спектра. Если эти области расположены в видимой части спектра, то вещество выглядит окрашенным. Цвет окраски – дополнительный, к поглощенному свету. Например, рубин поглощает в сине-зеленой области спектра, окраска рубина – красная.
В области полосы поглощения функции 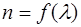 и
и 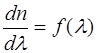 имеют существенно другой вид, чем вдали от этой полосы. Рассмотрим рис. 4.
имеют существенно другой вид, чем вдали от этой полосы. Рассмотрим рис. 4.
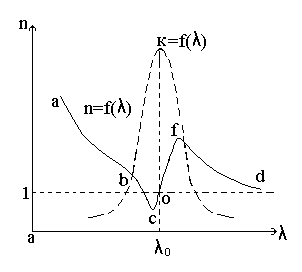 |
рис.4.
На участке (аb) показатель преломления уменьшается с ростом длины волны – нормальная дисперсия.
При приближении к области поглощения со стороны малых длин волн 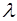 , показатель преломления n – с ростом длины волны
, показатель преломления n – с ростом длины волны 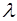 начинает сначала очень быстро уменьшаться (участок вс), достигая иногда значения меньше единицы, а затем, при переходе через полосу поглощения (участок сf), сильно возрастает переходя через точку О и достигает максимума (точка f). Затем вдали от полосы поглощения (участок fd), он ведет себя обычным образом, т.е. уменьшается с увеличением
начинает сначала очень быстро уменьшаться (участок вс), достигая иногда значения меньше единицы, а затем, при переходе через полосу поглощения (участок сf), сильно возрастает переходя через точку О и достигает максимума (точка f). Затем вдали от полосы поглощения (участок fd), он ведет себя обычным образом, т.е. уменьшается с увеличением 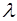 .
.
Поведение кривой 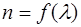 вблизи полосы поглощения описывает явление аномальной дисперсии (на рис. 4. – участок сf), т.е. в этой области спектра показатель преломления растет с ростом длины волны.
вблизи полосы поглощения описывает явление аномальной дисперсии (на рис. 4. – участок сf), т.е. в этой области спектра показатель преломления растет с ростом длины волны.
Аномальная дисперсия света в видимой области спектра наблюдается в тонких слоях сильных красителей (фуксин, цианин), а также в парах натрия и йода.
Надо отметить, что термин «аномальная дисперсия» не соответствует настоящему физическому смыслу и является неудачным. Он принят в силу исторических причин, так как впервые явление аномальной дисперсии было обнаружено только у одного вещества. В действительности аномальная дисперсия электромагнитных волн имеет место в любом веществе вблизи полосы поглощения, но эти полосы поглощения у прозрачных веществ лежат в невидимой для глаза области спектра. Например, у кварца – в инфракрасной, у стекла – в ультрафиолетовой.
В настоящей работе определение показателя преломления вещества основано на измерении угла наименьшего отклонения лучей в призме из данного вещества.
На рис. 5. – А- преломляющий угол призмы. Луч света идет по направлению В1ВСС1, 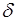 - угол отклонения луча. Угол
- угол отклонения луча. Угол 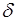 будет наименьшим, если
будет наименьшим, если
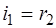 (4),
(4),
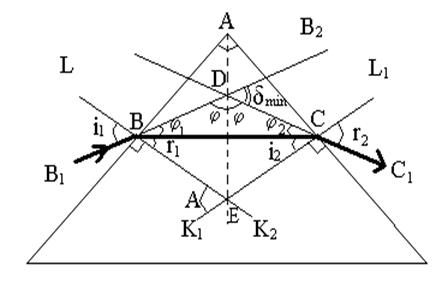 |
т.е. луч внутри призмы идет параллельно основанию.
Именно такой случай изображен на рис.5.
рис.5.
Так как по закону преломления
 , а
, а 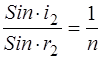
то получим: 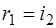 (5)
(5)
Угол отклонения 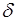 , являясь внешним углом треугольника DBC, равен сумме двух внутренних углов, с ним не смежных.
, являясь внешним углом треугольника DBC, равен сумме двух внутренних углов, с ним не смежных.
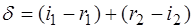
В силу равенства (4) и (5) получим:
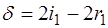 (6),
(6),
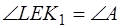 (7),
(7),
так как эти углы с взаимно перпендикулярными сторонами.
С другой стороны: угол
 (8),
(8),
как внешний угол треугольника ЕВС.
Из равенств (7) и (8) получаем: 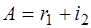 .
.
Отсюда, на основании равенства (5), имеем
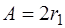 ;
; 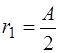 (9)
(9)
Из равенств (6) и (9) получаем:
 или
или 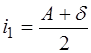 (10).
(10).
Подставляя значения  и
и  из формул (9) и (10) в выражение
из формул (9) и (10) в выражение 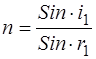 ,
,
находим, что
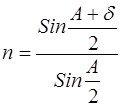 (11).
(11).
Из формулы (11) видим, что для определения показателя преломления вещества призмы нужно знать преломляющий угол призмы А и угол наименьшего отклонения 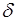 .
.
Определение угла 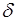 производится с помощью спектроскопа.
производится с помощью спектроскопа.
Методика измерений.
1. Перед коллиматором спектроскопа поместите спектральную трубку, наполненную водородом.
Примечание: электроды спектральной трубки соединяются со вторичной обмоткой трансформатора Румкорфа, первичная обмотка последнего соединяется с выпрямителем (12 В). Напряжение на выпрямитель подается через РНШ, до начала разряда в трубке.
Трубка устанавливается на штативе так, чтобы узкая часть находилась как раз перед щелью коллиматора, параллельно щели. Перемещением окуляра добейтесь отчетливой видимости спектральных линий и визирного острия.
2. С помощью микрометрического винта перемещайте зрительную трубку до тех пор, пока визирное острие не совместится с красной линией в спектре. По шкале микрометрического винта определите число делений N. Пользуясь градуировочным графиком 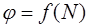 , определите угол
, определите угол 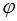 для данной линии (цена деления микрометрического винта – 0,02 мм).
для данной линии (цена деления микрометрического винта – 0,02 мм).
Переходя от яркой красной линии спектра к голубой и фиолетовой, определите углы 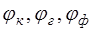 . Из рис.5. видно, что угол наименьшего отклонения равен
. Из рис.5. видно, что угол наименьшего отклонения равен 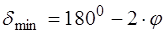 . Преломляющий угол данной призмы равен А=600. По формуле (11) определите показатели преломления стеклянной призмы для разных длин волн.
. Преломляющий угол данной призмы равен А=600. По формуле (11) определите показатели преломления стеклянной призмы для разных длин волн.
3. Для данной призмы постройте график зависимости 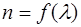 - дисперсионную кривую.
- дисперсионную кривую.
4. По дисперсионной кривой определите среднюю дисперсию D и коэффициент дисперсии ν (число Аббе).(не путать с частотой света)
ν 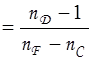 (12)
(12)
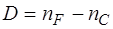 (13)
(13)
где 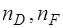 и
и 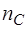 - показатель преломления для
- показатель преломления для  нм (среднее значение длины волны желтого дублета натрия),
нм (среднее значение длины волны желтого дублета натрия), 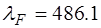 нм (голубая линия водорода),
нм (голубая линия водорода), 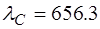 нм (красная линия водорода),
нм (красная линия водорода), 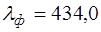 нм (фиолетовая линия водорода). Показатель преломления для желтой линии натрия
нм (фиолетовая линия водорода). Показатель преломления для желтой линии натрия 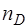 - определите из графика, зная длину волны для этой линии.
- определите из графика, зная длину волны для этой линии.
Средняя дисперсия D и коэффициент дисперсии 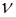 являются важными характеристиками оптических стекол. По значению параметров, полученных по формулам (12) и (13) в результате измерений, определите сорт стекла, из которого сделана призма (см. табл. в книге Л.Л. Гольдина «Руководство к лабораторным работам по физике»).
являются важными характеристиками оптических стекол. По значению параметров, полученных по формулам (12) и (13) в результате измерений, определите сорт стекла, из которого сделана призма (см. табл. в книге Л.Л. Гольдина «Руководство к лабораторным работам по физике»).
5. Все полученные результаты внесите в таблицу.
Таблица
| № | Nкр | Nг | Nф | 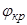
| 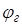
| 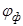
| 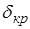
| 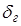
| 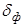
| 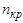
| 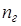
| 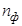
| 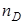
| D | ν | Сорт стекла |
| ср |
6. Начертить ход лучей в спектроскопе в рабочей тетради (см. приложение I) .
Контрольные вопросы.
1. Знать вывод формулы (11) для призмы.
2. Какой угол называется углом отклонения? При каких условиях он бывает максимальным или минимальным?
3. Какое явление называется дисперсией света?
4. Какая величина служит мерой дисперсии?
5. Какие виды дисперсии вы знаете? Чем они характеризуются?
6. Чем отличается спектры, полученные с помощью призмы из кронгласс или флинтгласс?
7. Закон Максвелла
8. Закон Кундта
9. Устройство и ход лучей в спектроскопе
10. Из электронной теории дисперсии рассмотреть: Какие силы действуют на электрон, входящий в состав атома, под действием внешних полей?
11. Иметь понятие о фазовой и групповой скорости.
12. Какими соотношениями связаны фазовая и групповая скорости при нормальной и аномальной дисперсии?
Литература:
1. Ландсберг Г.С. Оптика. -М.: Наука, 1976
2. Сивухин Д.В. Оптика. –М.: Наук, 1985
3. Фриш С.Э. и Тиморева А.В. Курс общей физики. т.III. М., 1961
4. Резников Л.И. Физическая оптика в средней школе.
5. Инструкция к спектроскопу.
6. Поглощение света в однородной поглощающей среде (рукопись).
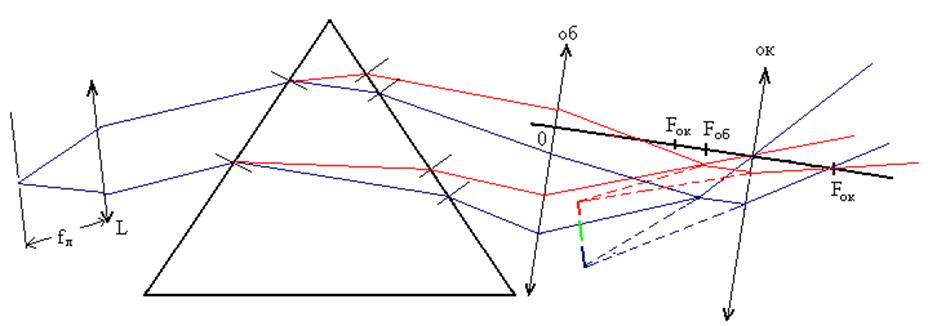
Приложение I.
Приложение II.
I. Индуктор высоковольтный. Назначение и устройство прибора.
Индуктор высоковольтный является источником тока высокого напряжения и применяется для демонстрации электрического разряда в воздухе, разрядов в вакуумных приборах (спектральных, ионных, катодных, рентгеновских трубок) и пр. Длина искры – до 100 мм.
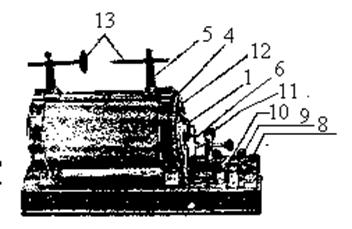 |
рис.1.
Прибор (рис. 1, 2, 3) представляет собой трансформатор с разомкнутой магнитной цепью и состоит из следующих частей: сердечника 1, собранного из полосок трансформаторного железа; первичной катушки 2, намотанной непосредственно на сердечник; вторичной обмотки высокого напряжения 3, одетой на первичную катушку; составного кожуха 4 с металлическими съемными борнами 5 для установки искровых разрядников 13, механического (пружинного) прерывателя 6; искрогасящего конденсатора 7, подключенного параллельно к прерывателю; пластмассовой подставки 8, на которую индуктор опирается двумя щечками 12, закрепленными винтами с гайками.
На подставке установлены две клеммы 9 от первичной катушки, к которым присоединяются провода от источника тока, и переключатель 10 для включения и изменения направления тока. Индуктор рассчитан на питание 10 – 12 в.
Подготовка к работе и работа с индуктором.
1. Разрядники индуктора закрепляют в борнах так, чтобы расстояние между концом иглы и плоскостью диска не превышало 100 мм.
2. Клеммы первичной катушки при помощи изолированных проводов соединяют с источником ВС-4÷12 В
3. Включают источник ВС-4÷12 В через РНШ (~150 В). Вращением регулировочного винта 14 приводят в действие прерыватель. Необходимо подобрать такой режим работы прерывателя, при котором искрение на его контактах будет минимальным. После этого винт закрепляют стяжным винтом 11 (рис.2.)
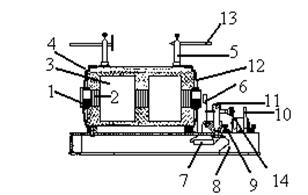 |
рис.2.
При нормальной работе индуктора между острием и диском разрядника, расположенными на расстоянии 100 мм, проскакивает яркая искра.
Для демонстрации вакуумных трубок их присоединяют тонкими проводами к борнам разрядника.
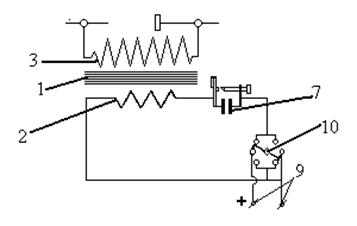 |
рис.3.
НЕ ДОПУСКАЕТСЯ:
1. Получать искру свыше 100 мм во избежание пробивания 
 изоляции внутри секций вторичной обмотки.
изоляции внутри секций вторичной обмотки.
2. Прикасаться руками к разряднику и борнам при работе индуктора.
3. Хранить индуктор при температуре свыше 400 С во избежание плавления парафиновой изоляции вторичной обмотки.
Приложение III.
Ввод формулы наименьшего угла отклонения в призме.(рис.5.)
 (1)
(1)
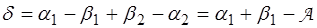 (2)
(2)
При изменении 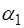 , будет меняться и
, будет меняться и 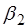 , а значит и угол отклонения
, а значит и угол отклонения 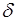 . Можно показать что угол
. Можно показать что угол 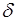 всегда остается большим некоторого минимального своего значения
всегда остается большим некоторого минимального своего значения 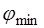 , т.е., что существует некоторое минимальное отклонение луча, прошедшего через призму.
, т.е., что существует некоторое минимальное отклонение луча, прошедшего через призму.
Докажем это.
Продифференцируем (2) по 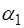 , тогда имеем:
, тогда имеем:
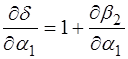
Для того, чтобы найти условие минимума отклонения, мы должны производную положить равной нулю 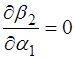 , тогда
, тогда
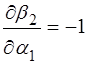 (3)
(3)
Дифференцируя (1) по 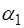 , имеем:
, имеем:
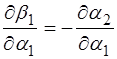 (4)
(4)
С другой стороны можно записать законы преломления для двух сторон призмы
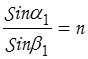 ;
; 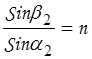
отсюда
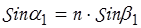 ;
; 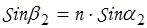
Дифференцируя по 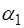 , имеем:
, имеем:
 ;
;
(5)
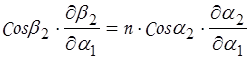
Подставляя в (5) из (3) и (4), получим:
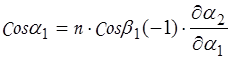 ;
;
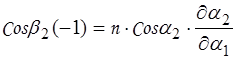
Или
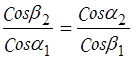
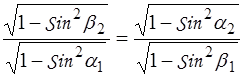
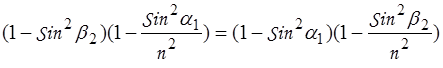
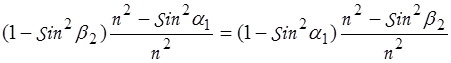 ;
;
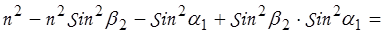
= 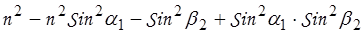 ;
;
или
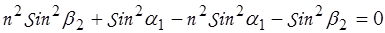
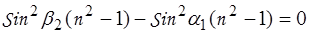
В результате преобразований получим:
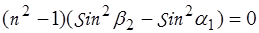
откуда 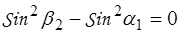
т.е. 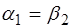 - это и есть условие минимума угла отклонения
- это и есть условие минимума угла отклонения 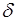 , следовательно, оно достигается тогда, когда углы, которые образуют падающий и выходящий лучи с нормалями к граням призмы, равны друг другу, так как преломляющий луч внутри призмы идет параллельно основанию.
, следовательно, оно достигается тогда, когда углы, которые образуют падающий и выходящий лучи с нормалями к граням призмы, равны друг другу, так как преломляющий луч внутри призмы идет параллельно основанию.
| <== предыдущая лекция | | | следующая лекция ==> |
| ОЧАГОВАЯ ПНЕВМОНИЯ | | | СОРТА ВИНОГРАДА |
Дата добавления: 2015-04-29; просмотров: 1299;
