Определение фокусного расстояния сферического зеркала

Обычно зеркала (плоские или сферические) для оптических систем изготавливают из стекла, на поверхность которых наносится испарением в вакууме или химическим путем слой металла (серебра, алюминия, меди), дающий высокий коэффициент отражения (ρ) света, т.е. ρ→1.

Наряду с таким способом применяется способ изготовления их из цельного куска металла, например, алюминия. такие отражатели большого размера могут быть применены для целей астрономии, в прожекторных системах.

Рассмотрим явление отражения света от сферического зеркала. Все рассуждения проведем для лучей, незначительно удаленных от оптической оси зеркала. Такие лучи называются параксиальными. В этом случае ввиду малости углов наклона световых лучей к оптической оси и нормали к отражающей поверхности можно заменить значения тангенсов и синусов этих углов значениями самих углов (в радиальной мере).

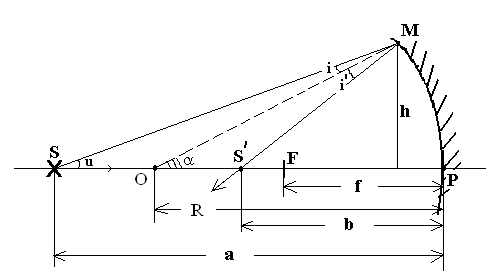рис.1

На рис.1 луч света от точечного источника S, лежащего на оптической оси ОР, падает на поверхность вогнутого зеркала в точку М под углом i к нормали и отражается от нее под углом i^/ (i=i^/). Нормаль к поверхности в точке М является радиусом R, проведенным из центра кривизны О зеркала в точку М. Отраженный в точке М луч пересекает оптическую ось в точке S^/. В свою очередь луч SР, идущий вдоль оптической оси, отразится в точке Р, являющейся вершиной зеркала, и пойдет обратно вдоль оптической оси. Следовательно, точка S^/ является изображением точки S.

Введенные на рис.1 обозначения имеют следующий смысл:

а=SР – расстояние от вершины зеркала до источника света;

в= S^/Р – расстояние от вершины зеркала до изображения источника;

R= ОМ=ОР – радиус кривизны зеркала(нормаль к ее поверхности);

f=FР – фокусное расстояние;

h –расстояние точки М от оптической оси.

Из треугольников SМО и ОМS^/ можно записать:

u+i=α (1)

u^/–i^/=α (2)

Сложив (4) и (5), получим:

u+ u^/=2α (3)

Для углов u, u^/ и α (ввиду их малости) можно записать:

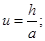
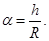
Подставляя значения этих углов в формулу (6), получим:

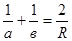(4)

Если а→ ∞, то в = 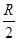. Точка F, в которой получается изображение, в этом случае называется главным фокусом зеркала. Расстояние f от точки F до вершины зеркала Р называется фокусным расстоянием, причем

F = 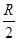. (5)

Величина, обратная фокусному расстоянию, называется оптической силой сферического зеркала

D = 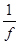. (6)

Из формул (5) и (6) имеем, что

D = 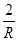, (7)

т.е. оптическая сила сферического зеркала зависит только от радиуса кривизны сферического зеркала.

Из формул (4) и (5) получим:

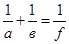. (8)

Физический смысл формулы (8):

при строго заданном положении предмета – положение изображения определяется однозначно.

Методика измерений.

Определить фокусное расстояние вогнутого сферического зеркала с помощью оптической скамьи.

Для этого: I) собрать установку согласно рисунку 2

1 2 3

рис.2

1- сферическое зеркало,

2- светящийся предмет, (напряжение на лампу 6В)

3- матовый экран.

2) Перемещая предмет или матовый экран вдоль направляющей, получить увеличенное изображение предмета. Измерения провести три раза при разных расстояниях между зеркалом и предметом. С помощью линейки и угольника измерьте в этих случаях расстояние от предмета до зеркала и от зеркала до изображения. Используя формулу (5) для сферического зеркала, определить его фокусное расстояние.

Данные занесите в таблицу 2.

Таблица 1

№ изм	а	в	F	∆F
сред.

3. Начертить все случаи получения изображения в сферических зеркалах (действительное – уменьшенное и увеличенное; мнимое – увеличенное и уменьшенное; предмет поместить в фокальную плоскость).