ОПРЕДЕЛЕНИЕ ФОКУСНОГО РАССТОЯНИЯ ЛИНЗ.

При прохождении света через границу двух сред (например, стекло-воздух) нарушается прямолинейность его распространения, и говорят, что лучи преломляются. Под лучом понимают направление распространения световой энергии. Совокупность лучей образует пучок. Если лучи при своем продолжении пересекаются в одной точке, то они называются гомоцентрическими. Пучок лучей, составляющий малый угол с оптической осью, называется параксиальным. Примером преломляющих поверхностей служат различные линзы.

Прямая, на которой лежат центры сферических поверхностей линзы, называется главной оптической осью линзы.

Лучи, падающие на линзу параллельно главной оптической оси, после преломления в линзе сходятся в одной точке, лежащей на главной оптической оси. Эта точка называется главным фокусом линзы. Расстояние от главного фокуса до оптического центра линзы называется фокусным расстоянием линзы. Плоскость, проходящая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. В зависимости от формы и среды, в которой они находятся, линзы делятся на собирающие (положительные) и рассеивающие (отрицательные). Линза называется тонкой, если толщина ее мала по сравнению с радиусом кривизны поверхности. Любой луч, проходящий через точку О практически не испытывает преломления. Эта точка О носит название оптического центра линзы (рис.1).

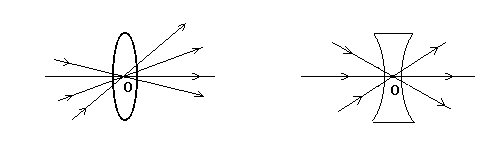
Рис.1.

Для вывода формулы тонкой линзы рассмотрим преломление на сферической поверхности. Пусть два однородных прозрачных вещества с показателями преломления n₁ = 1 иn разделены сферической поверхностью с радиусом кривизны r .

Проведем главную оптическую ось, которая соединяет точечный источник света S с центром кривизны сферической поверхности С₁ (рис.2).

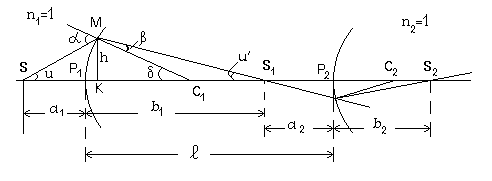
Рис.2.

Из точки S проведем любой параксиальный луч, падающий на сферическую поверхность в точке М. Прямая, соединяющая точки М и С₁, будет радиусом I-й сферической поверхности, а, следовательно, перпендикуляром к сферической поверхности. Обозначим угол падения луча SM на границу раздела через a , тогда по закону преломления преломляющий луч пересечет главную оптическую ось в точке S₁ , угол преломления обозначим через b .

По закону преломления ;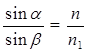

при n₁=1 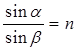. (1)

Углы между лучами: падающим, преломленным и главной оптической осью обозначим соответственно 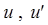. Угол между радиусом МС₁ и оптической осью через d

Для параксиальных лучей формула (1) будет иметь вид:

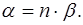(2)

Из SMC₁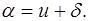

Из C₁MS₁ 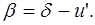(3)

Подставив (3) в (2), получим: 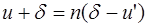. (4)

Из точки М опустим перпендикуляр МК на оптическую ось. Для параксиальных лучей Р₁К 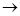О. Введем обозначения SP₁ =a ₁ ; P₁ S₁ =b ₁ ; P₁ C₁ = r₁ .

Из треугольников SMK, KMC₁ и KMS₁ имеем:

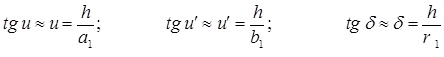(5)

Полученные значения углов (5) подставим в (4) и сразу левую и правую части сократим на h.

Тогда имеем:

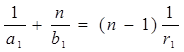(6)

Правая часть выражения (6) зависит только от радиуса кривизны и показателей преломления двух сред n₁ = 1 и n , т.е. в течение опыта остается величиной постоянной. Эта величина носит название оптической силы первой преломляющей поверхности и обозначается D₁ .

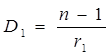. (7)

Eсли взять вторую сферическую преломляющую поверхность на границе раздела двух сред n и n₂ = 1, то точка S₁ будет уже предметом для второй преломляющей поверхности, а S₂ ее изображение (рис.2).

Проведя аналогичные рассуждения для второй сферической поверхности, получим:

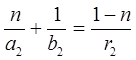, (8)

где

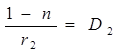(9)

- оптическая сила второй сферической преломляющей поверхности. Зная, что оптическая сила всей системы равна

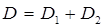, (10)

сложим левые и правые части выражений (6) и (8):

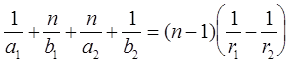. (11)

Обозначим расстояние Р₁ Р₂ = l , где l - толщина линзы.

Для тонких линз 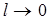, следовательно, выражение (11) запишется:

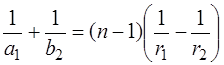. (12)

Правая часть выражения (12) называется оптической силой тонкой линзы

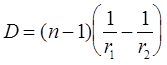. (13)

Физический смысл выражения (13) - оптическая сила не зависит от расстояний, а зависит только от формы линзы и показателей преломления линзы и окружающей среды.

Величина, обратная оптической силе линзы, называется фокусным расстоянием линзы. Если фокусное расстояние измеряется в метрах, то оптическая сила - в диоптриях.

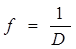. (14)

Подставляя выражения (13) и (14) в формулу (12), получим:

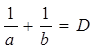, (15)

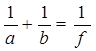. (16)

Физический смысл выражений (15) и (16) - если изменяется положение предмета относительно линзы, то положение изображения определяется однозначно. В формулах (15) и (16) используется следующее правило знаков: для всех действительных величин - их расстояния a ; b и f берутся со знаком "+"; для всех мнимых величин - знак "-".

Рассмотрим применение формулы (13) к линзе любого вида. Пусть нам дана линза с радиусами кривизны r₁ и r₂ .

Условимся считать r положительным, если световой пучок встречается с выпуклой сферической поверхностью, и r - отрицательным, если световой пучок падает на вогнутую поверхность.

На рис.3. показано получение выпукло-вогнутой линзы:

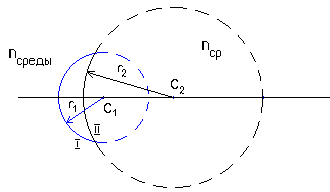
Рис.3.