Теорема о движении центра масс механической системы

Механическая система – любая совокупность взаимосвязанных между собой материальных точек. Действующие на механическую систему силы подразделяются на внешние ( 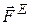) и внутренние ( 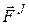), активные ( 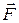) и реакции связей ( ).

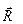Внешние силы – силы, действующие на точки (тела) механической системы со стороны точек (тел), не входящих в данную механическую систему. Внутренние силы – это силы взаимодействия между материальными точками (телами) самой механической системы.

В силу третьего закона Ньютона главный вектор и главный момент внутренних сил относительно произвольной точки O равны 0.

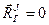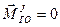; , (5.1)

Несмотря на это, движение системы происходит под действием внешних и внутренних сил.

Центром масс или центром инерции механической системы называется геометрическая точка, положение которой определяется радиусом-вектором:

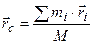, (5.2)

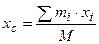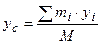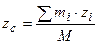, , , (5.3)

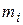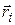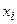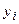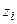где – масса i-й материальной точки системы; – радиус-вектор этой точки; , и – координаты точки, 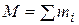– масса всей системы.

Теорема о движении центра масс звучит следующим образом: центр масс механической системы движется как материальная точка с массой равной массе всей системы, к которой приложены все внешние силы действующие на систему.

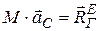. (5.4)

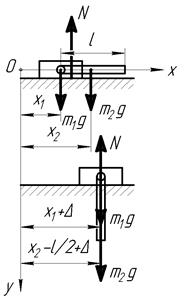
Из теоремы о движении центра масс механической системы следует, что движение всей механической системы можно рассматривать как движение одной точки – центра масс

Используя вышеописанные уравнения можно определять движение центра масс системы, не определяя движения отдельных ее точек.