Бинарные системы

В первой работе Хопфилда [6] функция F была просто пороговой функцией. Выход такого нейрона равен единице, если взвешенная сумма выходов с других нейронов больше порога T_j, в противном случае она равна нулю. Он вычисляется следующим образом:

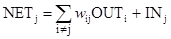, (6.1)

OUT, = 1, если NET_j>Т_j,

OUT. = 0, если NET_j<Т_j,

OUT не изменяется, если NET_j = Т_j,

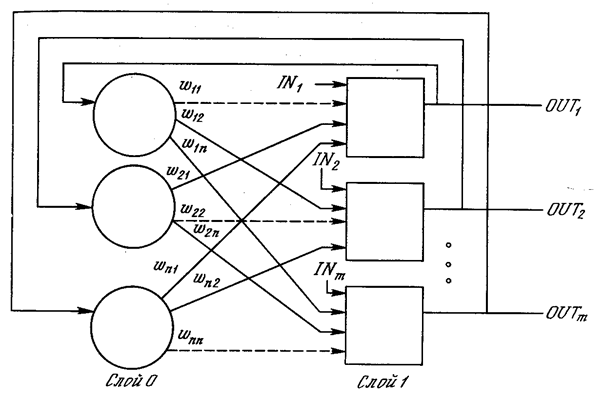
Рис. 6.1. Однослойная сеть с обратными связями.
Пунктирные линии обозначают нулевые веса

Состояние сети – это просто множество текущих значений сигналов OUT от всех нейронов. В первоначальной сети Хопфилда состояние каждого нейрона менялось в дискретные случайные моменты времени, в последующей работе состояния нейронов могли меняться одновременно. Так как выходом бинарного нейрона может быть только ноль или единица (промежуточных уровней нет), то текущее состояние сети является двоичным числом, каждый бит которого является сигналом OUT некоторого нейрона.

Функционирование сети легко визуализируется геометрически. На рис. 6.2а показан случай двух нейронов в выходном слое, причем каждой вершине квадрата соответствует одно из четырех состояний системы (00, 01, 10, 11). На рис. 6.2б показана трехнейронная система, представленная кубом (в трехмерном пространстве), имеющим восемь вершин, каждая из которых помечена трехбитовым бинарным числом. В общем случае система с n нейронами имеет 2ⁿразличных состояний и представляется n-мерным гиперкубом.

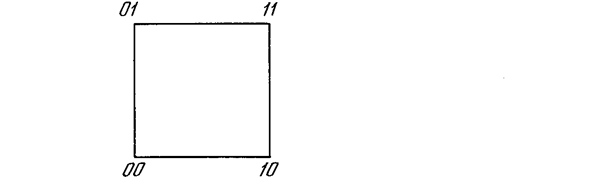
Рис. 6.2а. Два нейрона порождают систему с четырьмя состояними

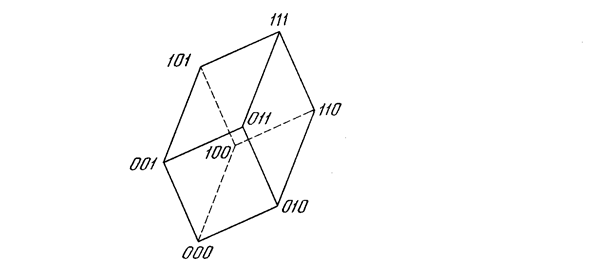
Рис. 6.2б. Три нейрона порождают систему с восемью состояниями

Когда подается новый входной вектор, сеть переходит из вершины в вершину, пока не стабилизируется. Устойчивая вершина определяется сетевыми весами, текущими входами и величиной порога. Если входной вектор частично неправилен или неполон, то сеть стабилизируется в вершине, ближайшей к желаемой.