Контроль изоляции по кривой напряжения саморазряда

После отключения изоляции от источника постоянного напряжения U (реле Р₁ и Р₂ на рис.6.5,а выключены) заряженные емкости слоев С₁ и С₂ неоднородной изоляции будут разряжаться на сопротивления утечки своих слоев R₁ и R₂, т.е. будет происходить постепенный саморазряд изоляции. Напряжение саморазряда на изоляции будет равно сумме напряжений на отдельных слоях изоляции, т.е. будет равно сумме экспонент:

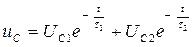. (4.3)

Если изоляция заряжалась в течение длительного времени, то напряжения на слоях в начальный момент времени будут прямо пропорциональны величинам активных сопротивлений слоев:

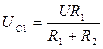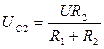; . (4.4)

Следовательно:

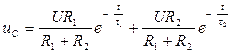. (4.5)

Если же изоляция разряжается после кратковременного подключения к источнику постоянного напряжения, то процесс саморазряда в этом случае будет описываться уравнением:

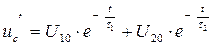(4.6)

Здесь: 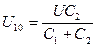; 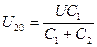. (4.7)

Следовательно:

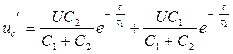. (4.8)

Отметим, что разность двух напряжений саморазряда u_c и 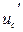дает значение возвратного напряжения. Действительно:

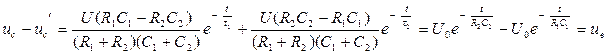(4.9)

Здесь: .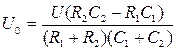

Пример 4.1.Определить напряжение саморазряда изоляции якоря тягового электродвигателя с параметрами, данными в примере 6.3 для двух случаев: длительного и кратковременного заряда изоляции от источника напряжения 1000В. По двум напряжениям саморазряда определить возвратное напряжение. По двум напряжениям саморазряда определить возвратное напряжение.

РешениеПри длительном заряде изоляции напряжения на слоях будут равны:

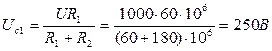
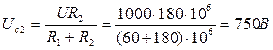
Напряжение саморазряда:

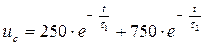(6-45)

При кратковременном заряде изоляции напряжения на двух слоях будут равны:

.

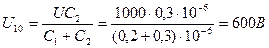
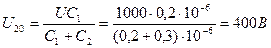Напряжение саморазряда

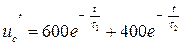(6-46)

На рис.6.7 приведены зависимости u_c и u_c^| , рассчитанные по формулам (6-45) и (6-46). Возвратное напряжение получается как разность этих напряжений (на рис.6.7 – это заштрихованная область):

.

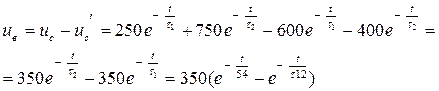Выражение для возвратного напряжения совпадает с полученным ранее в примере 4.1.