Скорость истечения и секундный расход идеального газа в сужающемся канале
При адиабатном истечении
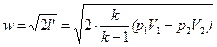, или 
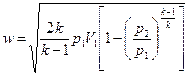. (9.14)
Массовый расход при истечении
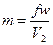, (9.15)
где f – площадь выходного сечения канала;
w – скорость истечения;
V2 – удельный объем газа в выходном сечении канала,
.
,
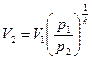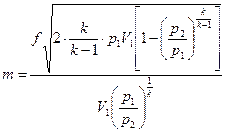или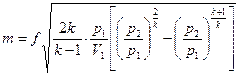 
. (9.16)
Графически располагаемая работа при истечении газа изображается площадью abcd
Анализ уравнения массового расхода идеального газа и критическое давление
;
.
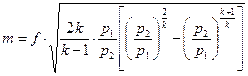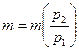Если р2 = р1 , то m = 0.
При уменьшении р2 расход m растет. При некотором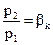 
расход достигает mmax, а затем уменьшается до m=0 при 
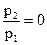, что противоречит здравому смыслу.
Представим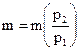 
на графике:
С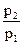 
m – кривая АК.
При 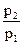= βк m = mmax.
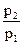При дальнейшем эксперимент дает m=const – кривая KD.
Расчет показывает m до m = 0 – кривая КВ.
Следовательно:
для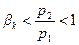 
– результаты расчета и эксперимента совпадают;
для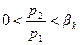 
– теория и опыт расходятся.
Сен-Венан и Вантдель предложили следующую гипотезу:
для 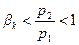давление в устье сужающегося канала равно давлению среды, куда проходит истечение, поэтому теория и опыт совпадают;
для 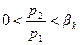давление в устье перестает быть равным давлению среды, в которую проходит истечение, даже, несмотря на понижение давления среды до полного вакуума давление в устье канала остается постоянным.
Определим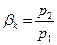 
, при котором m = mmax.
В уравнении (9.16) переменной величиной является
.
,
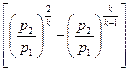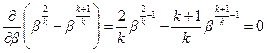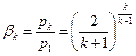. (9.17)
Для одноатомного газа к = 1,66 и βк = 0,49;
Для двухатомного газа к = 1,40 и βк = 0,528;
Для трёхатомного газа к = 1,33 и βк = 0, .
Определим критическое давление в выходном сечении сопла, при котором m = mmax:
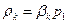. (9.18)
Критическая скорость и максимальный секундный расход идеального газа
Скорость газа, которая устанавливается в выходном сечени суживающегося канала при истечении газа в окружающую среду с давлением, равным или ниже критического называется критической скоростью.
Используя (9.14),заменив 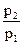величиной 
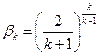,получим
,
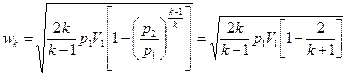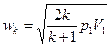. (9.19)
Из адиабатного процесса следует
.
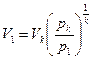Из уравнения (9.17) найдем
,
.
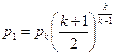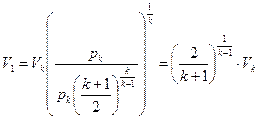Умножив левую и правую части на р1, получим
,
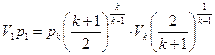подставив р1V1 в (9.19), получим wk:
,
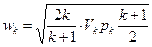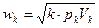, (9.20)
но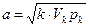 
, где а – скорость звука в газе в выходном сечении сужающегося канала, или критическая скорость при истечении газа равна местной скорости звука (в данном сечении), т. е. 
.
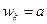Скорость истечения в выходном сечении сужающегося канала не может быть больще местной скорости звука в газе.
Заменим в (9.16) 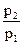на значение его из уравнения (9.17) , получим
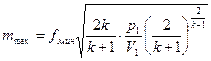. (9.21)
Основные условия течения идеального газа по каналам переменного сечения
Для стационарного режима уравнение неразрывности имеет вид
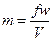или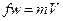 
.
При m = const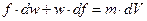 
,
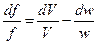. (9.22)
Уравнение (9.22) определяет условия неразрывности струн и показывает, что форма канала зависит от изменения объема газа и его скорости.
Исследуем это уравнение при адиабатном расширении идиального газа. Подставим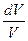 
из уравнения адиабаты, а 
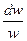из уравнения располагаемой работы
,
.
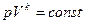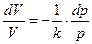Из уравнения (9.7) найдем
.
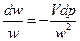Подставляя 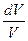и 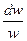в уравнение (9.22) получим
,
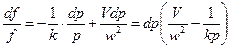или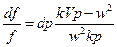 
, (9.23)
но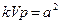 
, следовательно,
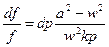. (9.23)
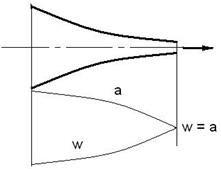
Пусть газ движется через сужающееся сопло, dp < 0. Из (9.24) следует, что знак df противоположен знаку (а2 – w2). Если (а2 – w2) > 0 и w < a, то df < 0, по направлению движения газа сечение сопла должно уменьшаться и скорость газа будет меньше местной скорости звука.
Если (а2 – w2) < 0 и w > a, то df > 0; по направлению движения газа сечение сопла должно увеличиваться и скорость газа будет больше местной скорости звука.
В узком сечении сопла скорость газа будет равна скорости звука. Для получения сверхзвуковых скоростей в соплах необходимо, чтобы они имели сначала суживающуюся часть, а затем расширяющуюся.
Пусть движение осуществляется через диффузор (dp > 0).
Если (а2 – w2) > 0 и w < a , то df > 0 ,
Если (а2 – w2) < 0 и w > a, то df < 0 .
Таким образом, в зависимости от скорости газа при входе один и тот же канал может быть и соплом и диффузором.
Случай истечения идеального газа из суживающегося сопла
1 Случай. Давление внешней среды больше критического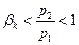 
.
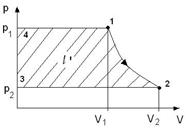
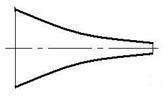
Происходит полное расширение газа, т.е. используется весь перепад давления от р1 до р2 .
Скорость газа в выходном сечении меньше скорости звука, w < a.
Давление газа в выходном сечении сопла равно давлению окружающей среды.
Скорость истечения и секундный расход определяются по формулам (9.14) и (9.16).
Площадь выходного сечения сопла f при заданном расходе определяется из формулы (9.16)
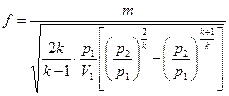(9.25)
l/=пл. 3124.
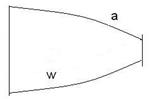
2 Случай. Давление внешней среды меньше критического, 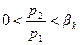. При этих условиях используется не весь перепад давления от р1 до р2 , а только часть от р1 до рк .
Происходит неполное расширение газа, скорость в выходном сечении суживающегося сопла равна критической скорости или местной скорости звука.
.
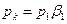Критическая скорость истечения и максимальный расход определяются по формулам (9.19) и(9.20.
При заданном расходе
.
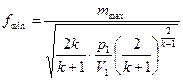l/ = пл. 1234.
Истечение идеального газа через комбинированное сопло Лаваля
Комбинированное сопло Лаваля предназначено для использования больших перепадов давления и для получения скоростей истечения, превышающих критическую или скорость звука.
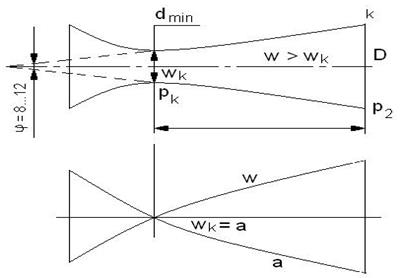
Сопло Лаваля состоит короткого суживающегося участка и расширяющейся конической насадки.
Угол конусности расширяющейся части должен быть равным φ = 8 .. 12 ˚. При φ > 12˚ наблюдается отрыв струи от стенок канала.
При истечении газа через комбинированное сопло в среду, где давление меньше критического в узком сечении сопла устанавливается критическое давление рк и критическая скорость wк.
В расширяющейся насадке сопла происходит дальнейшее увеличение скорости газа и падение давления до давления внешней среды.
При заданном f скорость истечения и секундный расход идеального газа определяются по формулам (9.14) и (9.16).
При заданном расходе
,
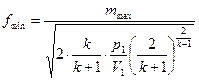а площадь выходного сечения равна
.
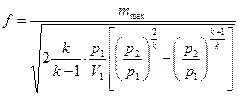Длина суживающейся части обычно берется равной диаметру выходного сечения сопла.
Длина расширяющейся чести определяется по формуле
,
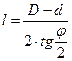где φ – угол конусности сопла;
D – диаметр выходного отверстия;
d – диаметр сопла в минимальном сечении.
Истечение газа с учетом трения
Приведенные выше скорости справедливы только для обратимого процесса истечения, т.к. не учитывают силы трения рабочего тела о стенки канала и внутреннее трение между струйками из-за разницы скоростей по сечению канала.
Отношение действительной скорости газа wД к теоретической w называют коэффициентом скорости, или скоростным коэффициентом
, 
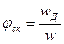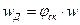(9.26)
РЕАЛЬНЫЕ ГАЗЫ И ПАРЫ
Дата добавления: 2015-04-03; просмотров: 4785;