Направления на земной поверхности
В самолетовождении принято направления на земной поверхности измерять в градусах относительно северного направления меридиана. Направления могут указываться азимутом (истинным пеленгом) и путевым углом.
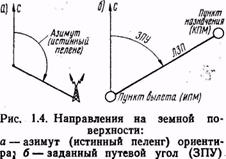 Азимутом, или истинным пеленгом, ориентира называется угол, заключенный между северным направлением меридиана, проходящего через данную точку, и направлением на наблюдаемый ориентир (рис. 1.4, а). Азимут (пеленг) ориентира отсчитывается от северного направления меридиана до направления на ориентир по часовой стрелке от 0 до 360°.
Азимутом, или истинным пеленгом, ориентира называется угол, заключенный между северным направлением меридиана, проходящего через данную точку, и направлением на наблюдаемый ориентир (рис. 1.4, а). Азимут (пеленг) ориентира отсчитывается от северного направления меридиана до направления на ориентир по часовой стрелке от 0 до 360°.
Для выполнения полета из одного пункта в другой их соединяют на карте линией, которая в самолетовождении называется линией заданного пути (ЛЗП). Чтобы выполнить полет по ЛЗП, необходимо знать направление полета, которое определяется заданным путевым углом (ЗПУ). ЗПУ — это угол, заключенный между 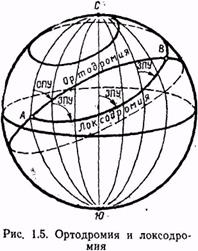 северным направлением меридиана и линией заданного шути (рис. 1.4, б). Он отсчитывается от северного направления меридиана до направления линии заданного пути по часовой стрелке от 0 до 360°.
северным направлением меридиана и линией заданного шути (рис. 1.4, б). Он отсчитывается от северного направления меридиана до направления линии заданного пути по часовой стрелке от 0 до 360°.
7. Ортодромия и локсодромия
Путь самолета между двумя заданными точками на карте может быть проложен по ортодромии или локсодромии. Выбор способа прокладки пути зависит от оснащенности самолета навигационным оборудованием. Каждая из указанных линий пути имеет определенные свойства.
Ортодромией называется дуга большого круга, являющаяся кратчайшим расстоянием между двумя точками А и В наповерхности земного шара (рис. 1.5).
Ортодромия обладает следующими свойствами:
1) является линией кратчайшего расстояния между двумя точками на поверхности земного шара;
2) пересекает меридианы под различными, неравными между собой углами вследствие схождения меридианов у полюсов.
Экватор и меридианы являются частными случаями ортодромии. Через две точки на земной поверхности, расположенные не на противоположных концах прямой, проходящей через центр Земли, можно провести только одну ортодромию. Условились путь самолета по ортодромии называть ортодромическим, а направление полета по ортодромии указывать ортодромическим путевым углом (ОПУ), заключенным между северным направлением меридиана и линией заданного пути в начальной точке ортодромии. В частном случае, когда ортодромия совпадает с меридианом или экватором, ортодромический путевой угол остается постоянным и равным в первом случае 0 или 180°, а во втором — 90° или 270°.
Полет по ортодромии с помощью магнитного компаса выполнить нельзя, так как в этом случае необходимо было бы изменять направление полета самолета от меридиана к меридиану, что осуществить практически невозможно. Поэтому такой полет выполняется с помощью специальных курсовых приборов — гирополукомпаса или курсовой системы.
На полетных картах, составленных в видоизмененной поликонической проекции, ортодромия между двумя пунктами, расположенными на расстоянии до 1000—1200 км, прокладывается прямой линией, а на больших расстояниях — кривой линией, обращенной выпуклостью к полюсу. В первом случае ОПУ и длина пути по ортодромии измеряется по карте. Во втором случае ортодромия наносится на карту по промежуточным точкам, а ОПУ и длина пути по ортодромии рассчитываются по специальным формулам.
В качестве исходных данных для математического расчета ОПУ и длины ортодромии служат географические координаты ее исходного и конечного пунктов. Эти координаты определяются с точностью до минуты по соответствующим справочникам или снимаются непосредственно на полетной карте.
Длина пути по ортодромии между двумя точками рассчитывается по формуле
cos Sорт = sinφ1 sinφ2 + cosφ1 cosφ2cos (λ2 — λ1),
где Sорт — длина пути по ортодромии в градусах дуги; φ1 и λ1— координаты исходной точки ортодромии; φ2 и λ2 — координаты конечной точки ортодромии.
Чтобы получить длину пути ортодромии в километрах, нужно полученный по формуле результат выразить в минутах дуги и умножить на 1,852 км.
Ортодромический путевой угол (направление ортодромии в исходной точке маршрута) рассчитывается по формуле
ctgα = cosφ1 tgφ2 cosec (λ2 — λ1)— sinφ, ctg(λ2 — λ1).
При большой протяженности ортодромия наносится на карту по промежуточным точкам. Координаты φ и λ этих точек рассчитываются по формуле
tgφ1= Аsin(λ — λ1) + Вsin(λ2 — λ), tgφ2
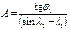
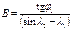
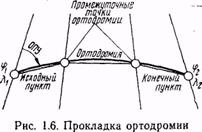 При этом обычно задаются долготой λ (через 10—20°) и определяют широту φ каждой промежуточной точки. Коэффициенты А и В для всех промежуточных точек остаются неизменными. Чтобы обеспечить высокую точность конечных результатов, расчет по указанным формулам ведется по пятизначным таблицам тригонометрических функций. По вычисленным координатам наносят промежуточные точки на карте, а затем через эти точки проводят ортодромию в виде плавной кривой линии (рис. 1.6) или в виде отрезков прямых, соединяющих вычисленные точки ортодромического пути.
При этом обычно задаются долготой λ (через 10—20°) и определяют широту φ каждой промежуточной точки. Коэффициенты А и В для всех промежуточных точек остаются неизменными. Чтобы обеспечить высокую точность конечных результатов, расчет по указанным формулам ведется по пятизначным таблицам тригонометрических функций. По вычисленным координатам наносят промежуточные точки на карте, а затем через эти точки проводят ортодромию в виде плавной кривой линии (рис. 1.6) или в виде отрезков прямых, соединяющих вычисленные точки ортодромического пути.
Математический расчет ортодромии дает хорошую точность, но связан с громоздкими вычислениями. Поэтому иногда ортодромию наносят на полетную карту при помощи навигационного глобуса или сетки, составленной в центральной полярной проекции, на которой ортодромия для любых расстояний изображается прямой линией. Используя это свойство сетки, можно произвести графический расчет ортодромии. Для этого на сетке соединяют начальную и конечную точки ортодромии прямой линией. На этой прямой намечают промежуточные точки. Затем по координатам переносят их на полетную карту и через полученные на полетной карте точки проводят ортодромию.
Полет из одной точки в другую по магнитному компасу удобно выполнять с постоянным путевым углом, т. е. по локсодромии.
Локсодромией называется линия, пересекающая меридианы под одинаковыми путевыми углами. Путь самолета по локсодромии называется локсодромическим. Постоянный угол, под которым локсодромия пересекает меридианы, называется локсодромическим путевым углом.
На поверхности земного шара локсодромия имеет вид пространственной логарифмической спирали, которая огибает земной шар бесконечное число раз и с каждым оборотом постепенно приближается к полюсу, но никогда не достигает его (см. рис. 1.5). Путь по локсодромии всегда длиннее пути по ортодромии. Только в частных случаях, когда полет происходит по меридиану или по экватору, длина пути по локсодромии и ортодромии будет одинаковой.
Если пункты перелета не очень удалены друг от друга, то разность пути по ортодромии и локсодромии незначительна. Разность также мала и при больших расстояниях полета, если маршрут проходит под углом не более, 20° по отношению меридиана. При больших расстояниях между пунктами перелета и особенно при направлении маршрута, близком к 90 или 270°, разность между расстояниями по ортодромии и локсодромии достигает больших значений. При большой протяженности маршрута путь по ортодромии значительно сокращает расстояние, уменьшает продолжительность полета и расход Топлива, что повышает полезную нагрузку самолета. Поэтому полеты сверхзвуковых транспортных самолетов выполняются по спрямленным воздушным трассам, совпадающим с ортодромиями.
Локсодромия обладает следующими свойствами:
1) пересекает меридианы под постоянным углом и на поверхности земного шара своей выпуклостью обращена в сторону экватора;
2) путь по локсодромии всегда длиннее пути по ортодромии, за исключением частных случаев, когда полет происходит по меридиану или по экватору. Параллели являются частными случаями локсодромии.
При полетах на большие расстояния разностью пути по ортодромии и локсодромии пренебрегать нельзя. Поэтому маршрут дальнего полета, если его промежуточные точки не определены заданием, должен прокладываться по ортодромии. В практике полетов по утвержденным воздушным линиям, Для которых установлены определенные правила, маршрут не является прямой от пункта вылета до пункта посадки, а имеет ряд изломов. Отрезки прямых выбирают с таким расчетом, чтобы разность в путевых углах в начале и конце участка не превышала 2°. При таком выборе длины участков ЛЗП прокладывается на полетной карте в виде прямой, которую принимают за локсодромию, если направление полета будет выдерживаться по магнитному компасу, или за ортодромию, если направление полета будет выдерживаться с помощью специальных курсовых приборов. В этом случае локсодромический путь будет незначительно отклоняться от прямой линии, и для отрезков 200—250 км практически будет совпадать с ЛЗП, проложенной на карте.
Дата добавления: 2015-04-21; просмотров: 1893;
