Кривые сушки и скорости сушки.

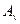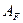Напряжение по влаге учитывает не только продолжительность процесса сушки конкретного материала (материал представляет собой субстанцию, состоящую из твердых частиц различной формы и размеров или листового материала), но и технологические параметры процесса, и принципиальные особенности сушильного аппарата. При расчете новых сушилок с помощью или для одного и того же материала необходимо, чтобы гидродинамические, температурные и другие условия были такими же, при которых определялось это напряжение по влаге.

Зная напряжение по влаге в форме 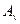, определяют рабочий объем сушильной камеры и ее геометрические размеры. Так, например, объем сушильного барабана может быть найден по формуле

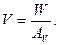Зная соотношение между длиной барабана и его диаметром, 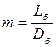, записывают 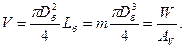Откуда: ;

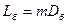
Такой прямой метод использования результатов эксплуатации сушильных аппаратов при решении задач проектирования обусловлен сложностью явлений процесса сушки влажных материалов: внутренней миграции влаги в материале, диффузии ее с поверхности в поток сушильного агента, сопутствующих физико-химических превращений (дегидратации, фазовых переходов), одновременного протекания теплопереноса, поведения единичного зерна в массе высушиваемых зерен.

Однако по мере проникновения в физическую сущность процесса возрастает роль теоретических построений. Они позволяют:

- грамотно поставить эксперимент;

- построить его физическую модель процесса;

- в отдельных (простых) случаях – математически описать и рассчитать процесс сушки (решить как задачу эксплуатации, так и задачу проектирования). В качестве примера рассмотрим далее – непрерывный процесс сушки в псевдоожиженном слое высушиваемого материала, как наиболее удобный своей простотой и возможностью (при значительных упрощениях) довести анализ до расчетных выражений.

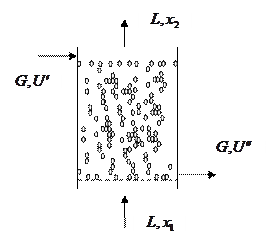Рис. Принципиальная схема сушильной установки с псевдоожиженным слоем высушиваемого материала.

Из общих соображений можно разделить процесс конвективной сушки на четыре стадии:

- 1^ая стадия - подвод влаги в зону сушки с влажным материалом;

- 2^ая стадия - диффузия влаги внутри ТМ из его внутренних областей к поверхности контакта с СА;

- 3^ья стадия - диффузия влаги с поверхности ТМ в поток сушильного агента;

- 4^аястадия - вывод влаги из рабочей (сушильной) зоны с СА.

Результирующая скорость сушки определяется интенсивностью каждой из этих стадий. Однако можно пойти по пути упрощения расчета, если скорость на какой-либо одной из стадий значительно меньше, чем на остальных. Тогда говорят, что эта стадия является лимитирующей. В таком случае расчету подлежит только эта стадия процесса, так как остальные в сравнении с ней протекают практически мгновенно.

Если в качестве лимитирующей стадии выступает 1^ая стадии, то речь идет о сушке в условиях потоковой задачи по ТМ, а интенсивность процесса сушки определяется уравнением материального баланса .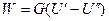

Если в качестве лимитирующей стадии выступает 2^ая стадия, то говорят о сушке в условиях внутренней задачи. В основе анализа этого случая лежит уравнение Фика. Для единичного сферического зерна радиусом R при симметричной сушке в случае постоянного коэффициента диффузии влаги в материале (D_M) в отсутствие химических превращений оно записывается в сферических координатах:

, где C – концентрация влаги в материале

Если в качестве лимитирующей стадии выступает 3^ая стадия, то говорят о сушке в условиях внешней задачи. Основное уравнение внешнего массопереноса имеет вид

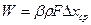, где 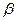- коэффициент массоотдачи; 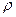- плотность а.с.в.; 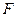- поверхность контакта фаз; 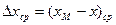- средняя движущая сила процесса, при 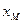- равновесное влагосодержание СА, .

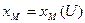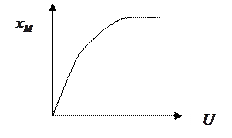
Рис. Равновесие при сушке.

Если в качестве лимитирующей стадии выступает 4^ая стадия, то речь идет о сушке в условиях потоковой задачи по СА. а интенсивность процесса сушки определяется уравнением материального баланса .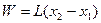

Заметим, что в обоих случаях сушки в условиях потоковой задачи по ТМ и СА уравнения материального баланса дополняются равновесным соотношением .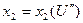

Видны очевидные упрощения при определении параметров сушки в условиях внутренней задачи, в самом деле: форма зерна может быть далека от сферической; коэффициент диффузии влаги в материале существенно зависит от ее концентрации в нем; при изменении С могут изменятся физическое состояние влаги в материале и характеристики ее диффузии, т.е. тогда D_М нельзя считать постоянным в ходе процесса сушки (по объему зерна – тоже). Тогда усложняется написание уравнение Фика, если возможно написание его вообще. Дополнительные затруднения – в установлении и математическом выражении зависимости D_М от С.

При сопоставимости скоростей хотя бы двух каких-либо медленных стадий задача именуется смешанной, ее расчет усложняется.

1 2 34

Дата добавления: 2015-04-03; просмотров: 778;