Сушка инертным газом.
Краткая характеристика расчетных методов сдвижений и деформаций земной поверхности
В период освоения новых месторождений полезных ископаемых приходится решать сложные технические вопросы, связанные с отработкой запасов под застроенными территориями и природными объектами, строительством предприятий, городов и поселков на подрабатываемых площадях, выбором трасс дорог, подземных коммуникаций и др.
Для решения этих вопросов необходимо иметь данные о параметрах и закономерностях процесса сдвижения в рассматриваемых условиях. Однако именно в этот период результатов наблюдений, как правило, не хватает и потому приходится использовать расчетные методы.
Разработаны методы расчета сдвижений и деформаций земной поверхности для одиночных выработок и при суммарном воздействии нескольких очистных выработок. В последнем случае необходимо учитывать активизацию сдвижений земной поверхности при повторных подработках толщи вследствие погашения расслоения и других пустот, образовавшихся ранее под влиянием отдельных выработок.
В зависимости от полноты исходных данных и получаемых результатов существующие методики расчета можно условно разделить на полные и сокращенные или, как их часто называют, упрощенные.
Полными методиками расчета определяются ожидаемые значения деформации, упрощенными — вероятные их значения. Исходными данными при всех методиках расчета являются мощность, глубина залегания и угол падения разрабатываемых пластов.
Для расчета по полной методике необходимо располагать дополнительными сведениями о горно-геологических условиях разработки пластов, в частности о размерах и местоположении очистных горных выработок, очередности отработки лав и пластов. Эти сведения содержатся обычно в календарных планах развития горных работ.
В зависимости от способа получения расчетных формул и степени их обоснованности методы расчета деформаций подразделяются на теоретические, эмпирические и полуэмпирические.
В инженерной практике используются в основном эмпирические и полуэмпирические методы расчета. Эмпирические методы базируются на зависимостях, полученных непосредственно из результатов инструментальных наблюдений в натурных условиях, полуэмпирические — на зависимостях, установленных на основании обобщений, теоретических соображений и математических аналогий, числовые значения параметров в которых определяются по данным натурных наблюдений. Четкую грань между этими методами провести очень сложно, особенно для полуэмпирических методов.
Значительная часть полуэмпирических методов расчета базируется на математических моделях процесса сдвижения. Этими методами определяются вертикальные и горизонтальные составляющие векторов сдвижения, на основании которых вычисляются линейные деформации как в вертикальном, так и в горизонтальном направлениях.
В качестве математических моделей процесса сдвижения получили распространение несколько гипотез.
Так, в основу гипотезы Р. Вальса (Германия) положен учет степени воздействия каждого элементарного объема пустоты на какую-либо точку массива или земной поверхности, которое предполагается аналогичным взаимодействию двух притягивающихся тел, т. е. обратно пропорционально квадрату расстояния от элемента выработки до рассматриваемой точки массива горных пород или земной поверхности.
Метод С. Кнотте (Польша) основан на предположении, что влияние каждого элементарного объема выработки можно характеризовать кривой распределения вероятностей (кривой Гаусса), а метод Е. Литвинишина (Польша) — на математической аналогии между явлениями сдвижения горных пород и теплопроводностью.
Р.А. Муллер, рассматривая породный массив как малосвязную среду, способную сопротивляться сжимающим и сдвигающим усилиям и лишь в незначительной степени — растяжению, определил напряженно-деформированное состояние двухслойного массива (коренные породы и наносы) вокруг выработки и получил формулы для расчета деформаций в условиях пологого падения пластов.
Весьма широкое применение в практике находят диаграммы сдвижения, которые строятся по данным натурных наблюдений, и представляют собой зависимости между величинами максимального оседания r|max и отношением D/H, где D— полудлина выработки, Н — средняя глубина работ (одна из таких диаграмм представлена на рис. 20.6).

 .
.
| 0,8 |
| 0,8 - |
| 0,4 - |

0 0,4 0,8 1,2 1,6 2,0 D/H
Рис. 20.6. Зависимость полного вектора сдвижений (в долях мощности пласта) от отношения размера выработки к глубине (диаграмма сдвижений)
Зависимости сдвижений и деформаций от параметров выработок и других горно-технических факторов, подобные приведенной на рис. 20.6, послужили основой составления типовых кривых сдвижений и деформаций, получивших широкое распространение в практике.
Широкую известность получил метод аналитического выражения профиля мульды оседания, состоящий в подборе уравнений, описывающих кривые оседания. При этом наклоны и кривизна мульды сдвижения определяются как первая и вторая производные от функции оседания.
В Верхней Силезии (Польша) и в каменноугольных бассейнах Венгрии профиль мульды оседания описывается экспоненциальной функцией, в бывшем СССР использовались преимущественно тригонометрические функции и функции Гаусса.
Методы расчета горизонтальных сдвижений и деформаций относительно надежно разработаны только применительно к слою пород, прилегающему к земной поверхности, а единой методики расчета сдвижений толщи горных пород в настоящее время нет. Существующие методы разработаны в основном применительно к конкретным практическим задачам. Так, при выборе мер охраны вертикальных шахтных стволов главное внимание уделяют расчетам растяжений и сжатий горных пород в вертикальном направлении и определению искривления стволов, а при проектировании горных работ вблизи водных объектов — расчетам горизонтальных деформаций и определению зоны и размеров секущих трещин.
Вместе с тем во многих методах имеются общие приемы и исходные принципы. В большинстве методов принято, что в толще горных пород слои перемещаются и деформируются над выработанным пространством (выше зоны обрушения) по тем же законам, что и на земной поверхности. При таком допущении расчет сдвижений по нормали к напластованию производят в каждом слое примерно так же, как на земной поверхности:
• вначале определяют границы влияния горных работ и положение точек с максимальными сдвижениями, т. е. размеры и местоположение полумульды;
• затем рассчитывают величины максимальных сдвижений и сдвижения в отдельных точках мульды;
• определяют значения наклонов и кривизны слоя как производные от кривой нормальных сдвижений.
Основные трудности при расчете сдвижений по изложенной методике состоят в определении границ области влияния горных работ. Иногда эту область ошибочно оконтуривают линиями, проведенными от границ горных работ под углами сдвижения или граничными углами, забывая, что указанные условные линии служат только для определения границ мульды сдвижения на земной поверхности.
В толще пород граница влияния горных работ имеет сложное очертание и пересекает разрабатываемый пласт не у границы выработанного пространства, а на некотором удалении от нее. В первом приближении область влияния горных работ (над выработанным пространством) можно оконтурить прямыми линиями, соединяющими границы мульды сдвижения на земной поверхности с границами зоны опорного давления, расположенной в плоскости пласта.
Расчет сдвижений и деформаций вдоль слоев представляет собой сложную и пока еще не всегда разрешимую задачу, так как для этих расчетов необходимо знать мощность пачек слоев, прогибающихся без расслоений (т. е. деформирующихся при подработке как одно целое, без сдвигов одной части относительно другой по поверхностям напластований и контактам), и положение нейтральной линии в каждой из этих пачек. Наиболее надежно указанные данные могут быть определены путем натурных наблюдений.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назовите основные термины и понятия.
2. Расскажите о параметрах процесса сдвижения горных пород пр и подземной разработке месторождений.
3. Каковы особенности развития процесса сдвижения горных пород' при подземной разработке различных классов месторождений?
4. Какие факторы определяют процесс сдвижения горных пород при подземной разработке?
5. Как наблюдают процессы сдвижения горных пород при подземной разработке?
6. Какие существуют расчетные методы определения параметров процессов сдвижения горных пород при подземной разработке?
Сушка.
1.4. Сушка с рециркуляцией отработанного воздуха, реальная, заданы точки «0», «2» и «М», а 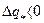 (или >0).
(или >0).
Начальный этап решения задачи заключается в построении линий смешения, нагрева и сушки идеального варианта (см. рис. 1.4).
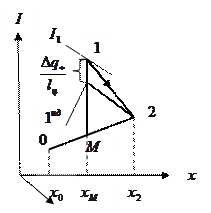 |
Рис. 1.4. Построение линии реальной сушки при известном значении 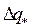 .
.
Запишем основное уравнение статики сушки применительно к данному варианту процесса
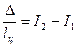 и найдем выражение для расчета I1
и найдем выражение для расчета I1
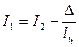 . Пусть
. Пусть 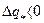 , тогда значение энтальпии в 1-ой точке реального процесса будет больше энтальпии во 1-ой точке процесса идеальной сушки на величину отношения. Отложим отрезок
, тогда значение энтальпии в 1-ой точке реального процесса будет больше энтальпии во 1-ой точке процесса идеальной сушки на величину отношения. Отложим отрезок 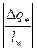 от т. «1ид» вверх по линии x = const. Найденная таким образом точка и есть точка «1» реального процесса сушки. Соединим т.т. «1» и «2». Линия «1-2» линия реального процесса сушки, а точнее линия изменения состояния влажного воздуха в сушильном аппарате в реальном процессе сушки. Эта линия проходит выше линии идеальной сушки, т.е. при
от т. «1ид» вверх по линии x = const. Найденная таким образом точка и есть точка «1» реального процесса сушки. Соединим т.т. «1» и «2». Линия «1-2» линия реального процесса сушки, а точнее линия изменения состояния влажного воздуха в сушильном аппарате в реальном процессе сушки. Эта линия проходит выше линии идеальной сушки, т.е. при 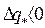 возрастает удельный расход тепла в калорифере.
возрастает удельный расход тепла в калорифере.
2.4. Многозональная идеальная сушилка с промежуточным нагревом воздуха между зонами (многоярусная ленточная сушилка).
Такой способ сушки применяется с целью понижения температуры воздуха на входе в зону сушки. На рисунке 2.4 показана принципиальная схема такой установки. Воздух последовательно проходит: калорифер первой зоны, сушильную камеру первой зоны; калорифер второй зоны, сушильную камеру второй зоны и т.д. На диаграмме Рамзина показано изменение параметров воздуха при прохождении его указанным маршрутом: «0-1» - нагревание воздуха в калорифере первой зоны; «1-2» сушка в первой зоне и т.д. Температура воздуха на входе в каждую из зон сушки одна и та же t1 = t3 = t5 . Температура воздуха на выходе из каждой зоны также одинакова: t2 = t4 = t6 . Следовательно, с увеличением числа зон процесс сушки в каждой из зон приближается к изотермическому режиму.
Сравнение многозональной сушилки с простой сушильной установкой (линии нагрева в калорифере и сушки, в сушильной камере которой показаны пунктирно) свидетельствует о снижение температуры сушильного агента на входе в сушильную камеру многозональной сушилки по сравнению с аналогичной величиной простой сушильной установки.
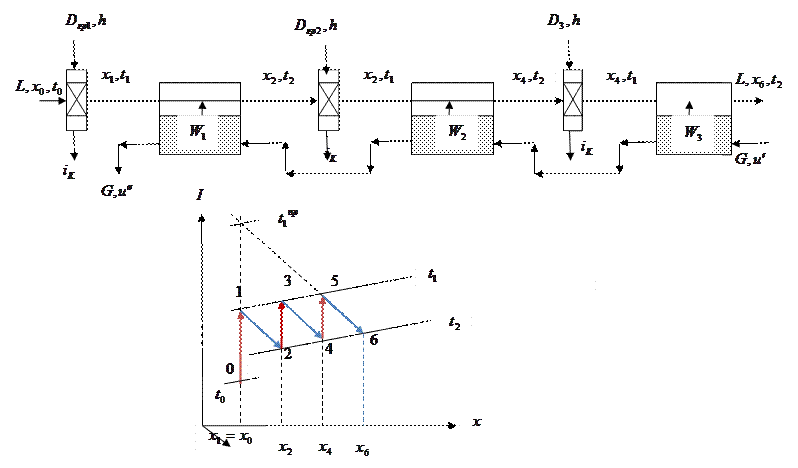
Рис. 2.4. Принципиальная схема многозональной идеальной сушильной установки. Графическая интерпретация процессов нагрева и сушки в такой установке.
2.4.1 Многозональная реальная сушилка с промежуточным нагревом воздуха между зонами (многоярусная ленточная сушилка).
Удельные потери теплоты каждой из зон пропорциональны потокам влаги W1, W2 и W3:
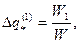
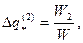
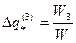 , где W1+ W2 +W3=W
, где W1+ W2 +W3=W
На рисунке 2.4.1. показана принципиальная схема реальной сушильной установки и геометрическая интерпретация процессов нагрева и сушки в такой установке. Видно, что в калориферах всех зон энтальпия СА на выходе выше энтальпии СА на выходе идеального варианта сушилки, т.к. qc каждой из зон равна нулю, а поэтому 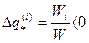 . Разность энтальпий СА на выходе из калорифера реальной сушилки и идеальной составляет
. Разность энтальпий СА на выходе из калорифера реальной сушилки и идеальной составляет
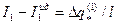 - для первой зоны;
- для первой зоны; 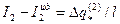 - для второй;
- для второй; 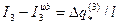 , где
, где
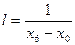
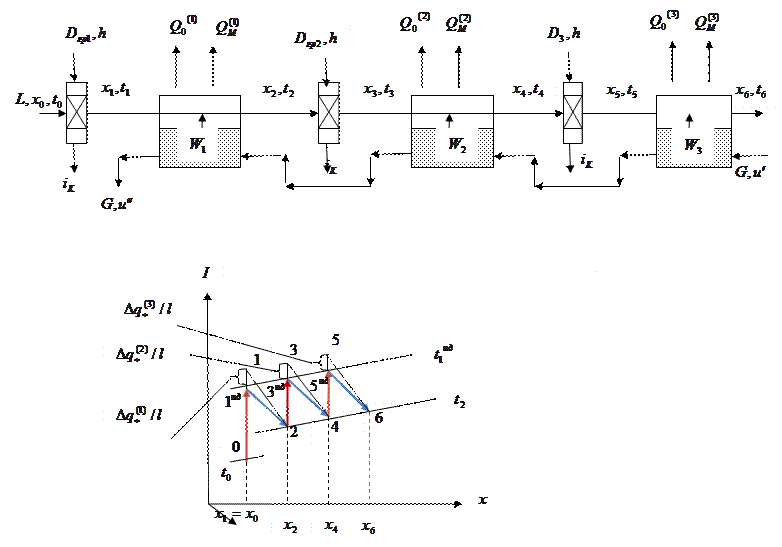
Рис. 2.4. Принципиальная схема многозональной реальной сушильной установки. Графическая интерпретация процессов нагрева и сушки в такой установке.
Сушка инертным газом.
Чтобы исключить контакт высушиваемого материала с кислородом воздуха прибегают к сушке инертным газом. Чаще всего в качестве инертного газа используют азот, который является основным компонентом воздуха. Поэтому при расчете технологических параметров используют диаграмму Рамзина.
На рисунке 3.4 представлена принципиальная схема сушильная установка с использованием в качестве СА инертный газ. СА циркулирует по контуру «калорифер – сушильная камера – конденсатор – вентилятор». Особенностью такой схемы является следующее обстоятельство. Так как СА, после прохождения через сушильную камеру, увлажняется, то для возврата его в процесс сушки требуется вывести из цикла поток влаги, поглощенный сушильным агентом в сушильной камере. С этой целью, в отличие от простой сушильной установки, при сушке инертным газом используют конденсатор, в котором сначала идет процесс охлаждения СА до относительной влажности в 100%, а далее идут одновременно два процесса: охлаждения СА и конденсация паров влаги до достижения исходных параметров СА.
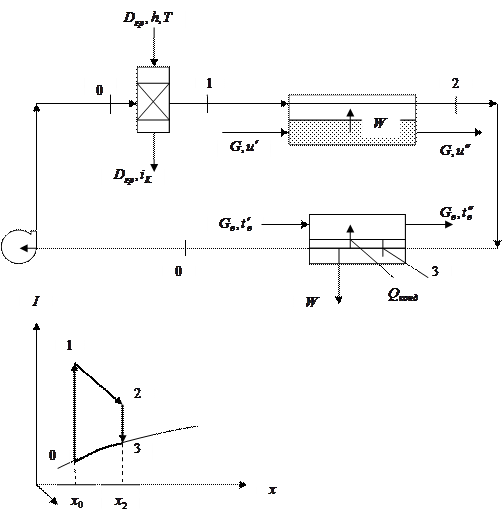 |
Рис. 3.4. Принципиальная схема сушильной установки с использованием в качестве СА инертного газа. Графическая интерпретация процессов, протекающих на каждом этапе контура, в координатах “I – x”.
Дата добавления: 2015-04-03; просмотров: 2364;
