Центральні проекції
Припустимо, що центр проекції перебуває в крапці 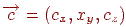 , а картинна площина збігається із площиною
, а картинна площина збігається із площиною  . Візьмемо довільну крапку зображуваного об'єкта
. Візьмемо довільну крапку зображуваного об'єкта 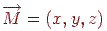 й визначимо її проекцію на обрану площину (мал. 9.7).
й визначимо її проекцію на обрану площину (мал. 9.7).
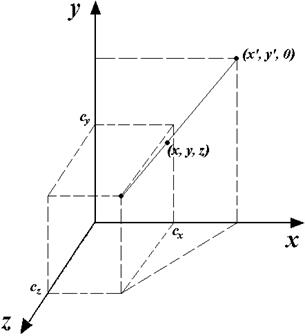
Рис. 9.7. Центральна проекція на площину XOY
Пряму, що проходить через крапки 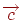 й
й 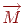 , задамо в параметричному виді:
, задамо в параметричному виді:
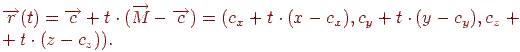
| (9.1) |
Тепер знайдемо крапку перетинання цій прямій з картинною площиною. Вона визначається з умови рівності нулю третьої координати:
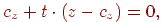
звідки визначаємо значення параметра 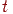 , при якому крапка прямої належить координатній площині:
, при якому крапка прямої належить координатній площині:
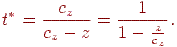
Підставляючи це значення у формулу (9.1), ми одержимо координати проекції крапки 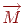 :
:
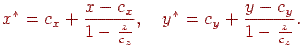
| (9.2) |
Фактором, що впливає на перспективну зміну розмірів, є наявність координати 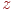 в знаменнику. Чим ближче виявляється крапка до центра проекції, тим більше знаменник, а відповідно й координати крапки.
в знаменнику. Чим ближче виявляється крапка до центра проекції, тим більше знаменник, а відповідно й координати крапки.
Ми будемо розглядати ситуацію, коли центр проекції лежить на осі 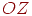 , а сама вісь спрямована від спостерігача до проекційної площини, тобто
, а сама вісь спрямована від спостерігача до проекційної площини, тобто 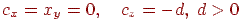 . Тоді формули (9.2) здобувають вид
. Тоді формули (9.2) здобувають вид
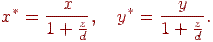
| (9.3) |
В однорідних координатах таке перетворення можна записати за допомогою двох операцій. Спочатку множимо матрицю проективного перетворення 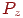 на вихідну точку й одержуємо крапку в четырехмерном просторі:
на вихідну точку й одержуємо крапку в четырехмерном просторі:
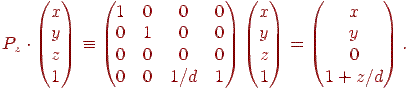
| (9.4) |
Потім проектуємо цю крапку в простір однорідних координат шляхом розподілу на четвертий компонент:
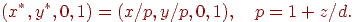
Подивимося тепер, що відбувається з пучком паралельних прямих під дією матриці проекції. Нехай заданий пучок прямих, паралельних вектору 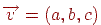 . Тоді параметричне рівняння прямої, що належить цьому пучку, має вигляд
. Тоді параметричне рівняння прямої, що належить цьому пучку, має вигляд
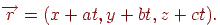
З формули (9.4) треба, що в результаті проектування одержимо безліч крапок
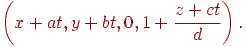
Переходячи до однорідних координат і помноживши чисельник і знаменник кожного дробу на 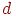 , одержимо крапки
, одержимо крапки  виду
виду
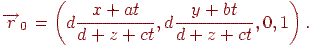
Тепер у кожному компоненті вектора чисельник і знаменник поділимо на 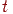 :
:
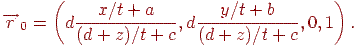
Переходячи до межі при  , одержимо крапку
, одержимо крапку

Таким чином, одержуємо, що після проектування пучок паралельних прямих перетинається в точці сходу 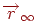 . Зрозуміло, що в кожного пучка своя крапка сходу. Якщо пучок прямих паралельний площини
. Зрозуміло, що в кожного пучка своя крапка сходу. Якщо пучок прямих паралельний площини  , тобто
, тобто  , то крапка сходу виявляється на нескінченності, а виходить, прямі залишаються паралельними.
, то крапка сходу виявляється на нескінченності, а виходить, прямі залишаються паралельними.
Для побудови перспективної проекції з декількома крапками сходу використовується матриця перспективного перетворення без проектування:
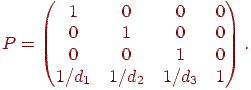
Тепер крапки простору спочатку піддаються перспективному перетворенню, а потім здійснюється проекція.
Визначимо крапки сходу для прямих, паралельних осям координат. Для прямих 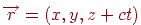 результатом проективного перетворення буде безліч крапок
результатом проективного перетворення буде безліч крапок 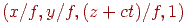 , де
, де 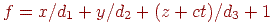 . При
. При  одержимо крапку з координатами
одержимо крапку з координатами 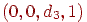 . При проекції на площину
. При проекції на площину  одержимо крапку
одержимо крапку 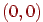 . Пучок прямих
. Пучок прямих 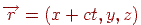 перейде в
перейде в  , а крапкою сходу для нього буде
, а крапкою сходу для нього буде 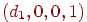 , що при проектуванні перейде в крапку, що лежить на осі
, що при проектуванні перейде в крапку, що лежить на осі 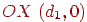 . Аналогічно для пучка прямих, паралельні осі
. Аналогічно для пучка прямих, паралельні осі 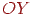 , одержимо крапку сходу на осі
, одержимо крапку сходу на осі 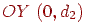 . Ці три крапки на площині є головними крапками сходу.
. Ці три крапки на площині є головними крапками сходу.
Дата добавления: 2015-04-03; просмотров: 1839;
