Ортогональні проекції
Спочатку розглянемо математичний опис паралельних проекцій як більше простих. Випадок, коли картинна площина перпендикулярна осі 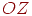 й задається рівнянням
й задається рівнянням  (тобто ортографическая проекція), фактично вже розглядався в лекції 4, де був наведений вид матриць проекції на координатні площини.
(тобто ортографическая проекція), фактично вже розглядався в лекції 4, де був наведений вид матриць проекції на координатні площини.
Випадок аксонометричної проекції зводиться до послідовності перетворень, подібно тому як здійснювався поворот у просторі щодо довільної осі. Нехай площина задається одиничним вектором нормалі 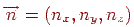 й відстанню від початку координат
й відстанню від початку координат  . Канонічне рівняння площини, таким чином, має вигляд
. Канонічне рівняння площини, таким чином, має вигляд
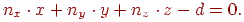
Вектор, спрямований по нормалі від початку координат до перетинання із площиною, є
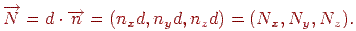
Координати вектора одиничної нормалі є її напрямними косинусами.
Проектування в просторі однорідних координат здійснюється наступною послідовністю кроків.
- Зрушення на вектор 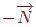 за допомогою матриці
за допомогою матриці
- 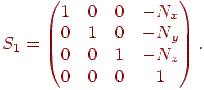
- Поворот, що сполучає напрямок нормалі з напрямком осі 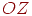 . Як було показано в лекції 4, цей поворот можна реалізувати у вигляді двох поворотів: перший (щодо осі
. Як було показано в лекції 4, цей поворот можна реалізувати у вигляді двох поворотів: перший (щодо осі 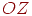 ) переводить нормаль у площину
) переводить нормаль у площину  , а потім - поворот щодо осі
, а потім - поворот щодо осі 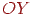 до сполучення нормалі з віссю
до сполучення нормалі з віссю 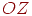 . Відповідну матрицю обертання, що є добутком двох матриць, позначимо
. Відповідну матрицю обертання, що є добутком двох матриць, позначимо 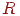 .
.
- Проекція на площину  за допомогою матриці
за допомогою матриці
- 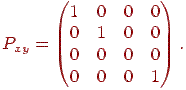
- Поворот за допомогою матриці 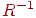 .
.
- Зрушення на вектор 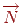 за допомогою матриці
за допомогою матриці 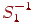
Повне перетворення, таким чином, визначається матрицею
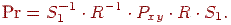
Дата добавления: 2015-04-03; просмотров: 1317;
