Метод двійкової розбивки простору
Тепер розберемо один спосіб використання методу художника при зображенні просторових сцен, що містять кілька об'єктів або складові об'єкти. Це так званий метод двійкової розбивки простору площинами. Площини, як звичайно, будуть задаватися за допомогою вектора нормалі 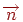 й відстані до початку координат
й відстані до початку координат 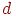 (з точністю до знака). Нехай зображувана сцена складається з набору непересічних граней
(з точністю до знака). Нехай зображувана сцена складається з набору непересічних граней 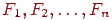 (вони можуть мати загальні прямолінійні ділянки границі). Проведемо площину
(вони можуть мати загальні прямолінійні ділянки границі). Проведемо площину 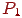 , що розбиває весь простір на два півпростори, в одному йз яких перебуває спостерігач. Припустимо, що площина при цьому не перетинає ні одну із граней (але може містити ділянку її границі). Тоді грані, що перебувають в одному півпросторі зі спостерігачем, можуть заслоняти від нього частина граней із другого півпростору, але не навпаки. Це означає, що вони повинні зображуватися пізніше. Розіб'ємо площиною
, що розбиває весь простір на два півпростори, в одному йз яких перебуває спостерігач. Припустимо, що площина при цьому не перетинає ні одну із граней (але може містити ділянку її границі). Тоді грані, що перебувають в одному півпросторі зі спостерігачем, можуть заслоняти від нього частина граней із другого півпростору, але не навпаки. Це означає, що вони повинні зображуватися пізніше. Розіб'ємо площиною 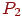 другий півпростір і знову визначимо, яка група граней з нього повинна зображуватися раніше. Продовжуючи цей процес до того рівня, коли весь простір буде розбито площинами на секції, у кожній з яких буде перебувати тільки одна грань, ми одержимо впорядкований набір граней. Цей порядок можна зобразити у вигляді двійкового дерева. У контексті розглянутого алгоритму це дерево являє собою структуру даних
другий півпростір і знову визначимо, яка група граней з нього повинна зображуватися раніше. Продовжуючи цей процес до того рівня, коли весь простір буде розбито площинами на секції, у кожній з яких буде перебувати тільки одна грань, ми одержимо впорядкований набір граней. Цей порядок можна зобразити у вигляді двійкового дерева. У контексті розглянутого алгоритму це дерево являє собою структуру даних 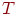 , елементами якої є покажчик на грань зображуваної сцени, площина, що відокремлює цю грань, покажчики на ліве й праве поддерево
, елементами якої є покажчик на грань зображуваної сцени, площина, що відокремлює цю грань, покажчики на ліве й праве поддерево  й
й  . Такий елемент називається вузлом дерева.
. Такий елемент називається вузлом дерева.
У кожному вузлі дерева ліве поддерево буде містити грані, відділені площиною, а праве - не відділені. Малювання сцени здійснюється за допомогою рекурсивного алгоритму наступного виду:

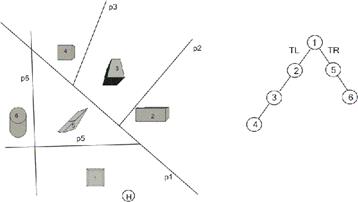
Рис. 8.6. Розбивка простору й відповідне йому дерево
Побудова площин і дерева в цьому випадку здійснюється "вручну". Для ефективності роботи алгоритму треба прагнути до того, щоб дерево було збалансованим. Якщо якісь грані не вдається відокремити, то їх перетинають площинами й малюють як два об'єкти. Спосіб визначення, по яку сторону площини перебуває спостерігач, а по яку - грань, дуже простий. Параметр площини 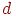 для кожної грані будемо задавати так, щоб грань перебувала в позитивній напівплощині. Тоді якщо при підстановці координат спостерігача в це рівняння одержуємо позитивне значення, то він перебуває в одній напівплощині із гранню, якщо ні, те в різні.
для кожної грані будемо задавати так, щоб грань перебувала в позитивній напівплощині. Тоді якщо при підстановці координат спостерігача в це рівняння одержуємо позитивне значення, то він перебуває в одній напівплощині із гранню, якщо ні, те в різні.
Алгоритм може застосовуватися не тільки до багатогранників, але й взагалі до будь-якої сцени за умови, що є алгоритм зображення складових її об'єктів. На мал. 8.6 зображена проекція сцени, розбитої вертикальними площинами, і відповідне їй дерево. Положення спостерігача відзначене кружком з буквою Н. При цій точці зору об'єкти будуть зображуватися в послідовності 5, 6, 1, 2, 3, 4.
Дата добавления: 2015-04-03; просмотров: 1166;
