Алгоритм Робертса

Цей алгоритм, запропонований в 1963 р., є першою розробкою такого роду й призначений для видалення невидимих ліній при штриховому зображенні об'єктів, складених з опуклих багатогранників. Він ставиться до алгоритмів, що працюють в об'єктному просторі, і дуже елегантний з математичної точки зору. У ньому дуже вдало сполучаються геометричні методи й методи лінійного програмування.

Опуклий багатогранник однозначно визначається набором площин, що утворять його грані, тому вихідними даними для алгоритму є багатогранники, задані списком своїх граней. Грані задаються у вигляді площин, заданих у канонічній формі (див. лекцію 3) в об'єктній системі координат: .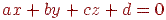

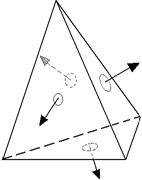
Рис. 8.2. Зовнішні нормалі тетраедра

Таким чином, кожна площина визначається четырехмерным вектором 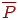, а кожна крапка 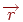, задана в однорідних координатах, також являє собою четырехмерный вектор:

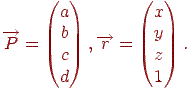
Приналежність крапки площини можна встановити за допомогою скалярного добутку, тобто якщо 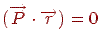, те крапка належить площини, якщо ж ні, те знак добутку показує, по яку сторону від площини ця крапка перебуває. В алгоритмі Робертса площини будуються таким чином, що внутрішні крапки багатогранника лежать у позитивній напівплощині. Це означає, що вектор є зовнішньою нормаллю до багатогранника (мал. 8.2). 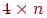З векторів площин будується прямокутна матриця порядку , що називається узагальненою матрицею опису багатогранника:

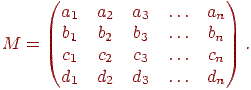
Множачи стовпці матриці на вектор 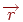, одержимо n-мірний вектор, і якщо всі його компоненти ненегативні, то крапка належить багатограннику. Ця умова будемо записувати у вигляді 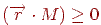(мається на увазі множення вектор-рядка на матрицю).

У своєму алгоритмі Робертс розглядає тільки відрізки, що є перетинанням граней багатогранника.

З узагальненої матриці можна одержати інформацію про те, які грані багатогранника перетинаються у вершинах. Дійсно, якщо вершина 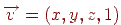належить граням 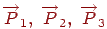, то вона задовольняє рівнянням

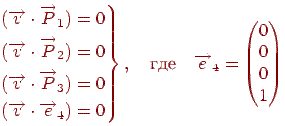
Цю систему можна записати в матричному виді:

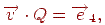
де 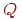- матриця, складена з вектор-стовпців 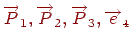. Виходить, координати вершини визначаються співвідношенням

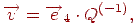
т.е. вони становлять останній рядок зворотної матриці. А це означає, що якщо для яких-небудь трьох площин зворотна матриця існує, то площини мають загальну вершину.

Алгоритм насамперед видаляє з кожного багатогранника ті ребра або грані, які екрануються самим тілом. Робертс використовував для цього простий тест: якщо одна або обидві суміжні грані звернені своєю зовнішньою поверхнею до спостерігача, то ребро є видимим. Тест цей виконується обчисленням скалярного добутку координат спостерігача на вектор зовнішньої нормалі грані: якщо результат негативний, то грань видима.

Потім кожне з видимих ребер кожного багатогранника рівняється з кожним з багатогранників, що залишилися, для визначення того, яка його частина або частини, якщо такі є, екрануються цими тілами. Для цього в кожну крапку ребра проводиться відрізок лучачи, що виходить із крапки розташування спостерігача. Якщо відрізок не перетинає жодного з багатогранників, то крапка видима. Для рішення цього завдання використовуються параметричні рівняння прямої, що містить ребро, і лучачи.

Якщо задані кінці відрізка 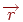й 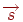, а спостерігач розташований у крапці 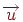, то відрізок задається рівнянням

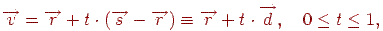
а пряма, що йде в крапку, що відповідає параметру , - рівнянням

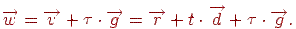
Для визначення тої частини відрізка, що закривається яким-небудь тілом, досить знайти значення 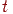й 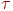, при яких добуток вектора 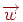на узагальнену матрицю позитивно. Для кожної площини 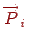записується нерівність

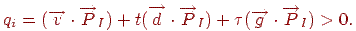
Ці умови повинні виконуватися для всіх площин.

Думаючи 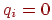, одержуємо систему рівнянь, рішення якої дають нам крапки "зміни видимості" відрізка. Результат можна одержати шляхом спільного рішення всіляких пар рівнянь із цієї системи. Число всіляких рішень при 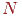площинах дорівнює .

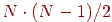Тому що обсяг обчислень росте зі збільшенням числа багатокутників, те бажано в міру можливості скорочувати їхнє число, тобто якщо ми апроксимуємо деяку поверхню багатогранником, то як грані можна використовувати не трикутники, а більше складні багатокутники. При цьому, зрозуміло, встає проблема, як побудувати такий багатокутник, щоб він мало відхилявся від плоскої фігури.