Додаткові теоретичні відомості. Клас то́чності — це задане у відсотках відношення допустимої основної абсолютної похибки вимірювального приладу в робочій частині шкали до верхньої межі
Клас то́чності — це задане у відсотках відношення допустимої основної абсолютної похибки вимірювального приладу в робочій частині шкали до верхньої межі діапазону вимірювань.
Основною похибкою називається похибка при нормальних умовах роботи приладу (певна температура, нормальне положення приладу, відсутність магнітних і електричних полів і т.д.). Причинами основної похибки є тертя в опорах рухомої частини приладу, неточність градуювання і нанесення шкали і т.д. Робочою частиною у випадку рівномірної шкали є вся шкала, для нерівномірної — від 25% до 100% від верхньої межі шкали.
Додаткові похибки вимірювальних приладів, які залежать від зміни температури, частоти струму, положення приладу, впливу зовнішніх магнітних полів та ін., не повинні перевищувати значення класу точності.
Клас точності — це узагальнена характеристика засобу вимірювальної техніки, що визначається границями його допустимих основних і додаткових похибок, а також іншими характеристиками, що впливають на його точність, значення яких регламентуються стандартами на окремі види засобів вимірювань.
Наприклад, якщо манометр на верхню межу вимірювання 500 кгс/см² має клас точності 2, то це означає, що максимально можлива похибка становить 2 відсотки від 500 кгс/см², що відповідає абсолютній похибці в 10 кгс/см².
Значення класу точності відповідно до стандарту, як правило є написане на шкалі приладів. Залежно від ступеня точності показів вимірювальні прилади поділяються на сім класів, що позначаються відповідно числами: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Клас точності приладу вказується на його шкалі числом, вміщеним всередині кола[2]. Промислові прилади, зазвичай мають наступні класи точності: 0,5; 1,0; 1,5; 2,5; 4,0.
Класи точності цифрових вимірювальних приладів із вбудованими обчислювальними пристроями для додаткової обробки результатів вимірювань слід встановлювати без урахування режиму обробки.

Для встановлення похибок засобу вимірювання, він періодично повіряється зразковими засобами, які за класом точності на декілька класів вищі. Повірка проводиться спочатку при збільшенні вимірюваної величини (прямий хід), а потім при її зменшенні (зворотний хід). Якщо при повірці приладу встановлено, що найбільша приведена похибка не перевищує або дорівнює класу точності, то прилад визнається придатним для подальшої експлуатації.
Ціна́ по́ділки шкали́ (ста́ла при́ладу) аналогового вимірювального приладу — різниця значень вимірюваної величини, що відповідає двом сусіднім позначкам шкали.
Приклад. Якщо наконечник індикатора годинникового типу перемістити на 0,01 мм, то стрілка зсунеться на одну поділку великої кругової шкали, отже, ціна поділки складає 0,01 мм (див. рисунок).
Ціна поділки залежить від верхньої і нижньої межі вимірювання приладу і від числа поділок шкали. Особливо це треба мати на увазі тоді, коли використовується при вимірюванні прилад, в якого верхня межа вимірювань має декілька значень.
Величина, обернена до сталої приладу, називається чутливістю приладу. Чутливість приладу визначається відношенням збільшення кутового або лінійного переміщення покажчика приладу в градусах, міліметрах або просто в поділках шкали до відповідного збільшення тієї величини, що вимірюється.
В цифрових вимірювальних приладах (приладах з цифровим табло) метрологічною характеристикою, за замінює ціну поділки шкали є крок дискретності.
Багатомежні прилади – це такі прилади, які дозволяють розширювати межи вимірювання за рахунок зміни ціни поділки. Сучасні багатомежні прилади також надають можливість вимірювання як, наприклад, напруги, так і сили струму, тощо. При переході з однієї межі у іншу, багатомежний прилад змінює свою чутливість за рахунок ціни поділки.
Слід пом’ятати, що амперметр потрібно під’єднувати послідовно зі споживачем; а вольтметр – паралельно.
Найпростіше електричне коло може складатися з джерела струму, споживача опору R, з’єднувальних провідників, амперметра і вольтметра.
Закон Ома для ділянки електричного кола: на деякій ділянці кола сила струму I прямо пропорційна напрузіU і обернено пропорційна опору R ділянки:
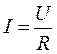
Перший закон Кірхгофа (Закон струмів Кірхгофа) говорить, що алгебраїчна сума струмів, що збігаються у вузлі ланцюга дорівнює нулю (значення випливають струмів беруться зі зворотним знаком):
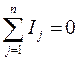
Іншими словами, скільки струму втікає у вузол, стільки з нього і випливає. Даний закон випливає з закону збереження заряду. Якщо ланцюг містить p вузлів, то вона описується p - 1 рівняннями струмів. Цей закон може застосовуватися і для інших фізичних явищ (наприклад, водяні труби), де є закон збереження величини і потік цієї величини.
Другий закон Кірхгофа (Закон напруг Кірхгофа) говорить, що алгебраїчна сума падінь напружень по будь-якому замкнутому контуру кола дорівнює алгебраїчній сумі ЕРС, що діють уздовж цього ж контура. Якщо в контурі немає ЕРС, то сумарне падіння напруги дорівнює нулю:
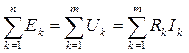
Лабораторна робота №2
«Визначення опору методом мостової схеми»
Мета роботи: Вивчити метод мостової схеми і визначити невідомі опори цим методом.
Прилади і приналежності:відомий опір (R=470 Ом), невідомі опори (Rx1, Rx2, Rx3); реохорд і гальванометр (нуль-індикатор); джерело постійної напруги.
Теоретичні відомості.Одним з найбільших точних методів вимірювання опорів є метод моста Уітстона. Схема моста Уітстона зображена на рисунку. Між клемами А і В закріплено калібровий дріт-реохорд, що має рухомий контакт D; І – постійний струм від джерела постійного струму; R – відомий еталонний опір; Rx – невідомий опір; Г – гальванометр; l1 i l2 – плечі реохорда (довжина дроту).
Метод вимірювання опору при допомозі моста Уітстона засновано на порівнянні невідомого опору з відомим опором. Нехай струм в плечах моста і в діагоналі CD спрямовані так, як показано на рис.1, тоді, згідно правилам Кирхгофа для розгалуженого кола, можна скласти такі 5 рівнянь з п’ятьма невідомими:
Для вузла С: Іх-Іх-Іх=0 (1)
Для вузла D: I1-I2-Ir=0 (2)
Для контура ACDA: IxRx+IrRr=I1R1 (3)
Для контура ABEA: I1R1+I2R2=U (4)
Для контура CBDC: IR-I2R2-IrRr=0 (5)
Де Rr – опір гальванометра; R2 і R1 – опір «плечей» l1 i l2 – реохорда.

Змінюючи положення рухомого контакту D реохорда ( і таким чином змінюючи співвідношення між l1 i l2), можливо домогтися того, щоб потенціал точки D дорівнював би потенціалу точки С ( 

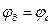 )
)
В цьому випадку струм через гальванометр не іде (міст збалансовано). Враховуючи це (Ir=0), рівняння (1-5) можна спростити:
Ix=Ir (6)
I1=I2 (7)
IxRx=IxRx (8)
IR=I2R2 (9)
Поділивши два основні рівняння одне на одне отримаємо:
 (10)
(10)
Враховуючи співвідношення (6) і (7) вираз (10) можна спростити:
 (11)
(11) 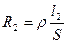 , (12)
, (12)
де  - питомий опір дроту реохорда; S – площа поперечного перерізу дроту.
- питомий опір дроту реохорда; S – площа поперечного перерізу дроту.
Підставляючи значення R2 і R1 в співвідношення (11), отримаємо формулу для визначення питомого опору:
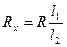
Таким чином, підібравши відповідну довжину «плечей» реохорда l1 i l2 і знаючи еталонний опір R,можна знайти Rx.
Дата добавления: 2015-04-19; просмотров: 1820;
