Метод условной линеаризации
Метод условной линеаризации применяется в случаях, когда в нелинейном уравнении одно из слагаемых в левой части мало по сравнению с другими, вследствие чего, без внесения существенной погрешности, его можно соответствующим образом линеаризовать. Благодаря этому все уравнение становится линейным для одной из переменных, определяющих характеристику 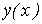 нелинейного элемента, например
нелинейного элемента, например 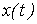 . С использованием этой характеристики находится затем временная зависимость
. С использованием этой характеристики находится затем временная зависимость 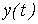 для второй определяющей ее переменной по алгоритму:
для второй определяющей ее переменной по алгоритму:
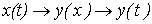 .
.
Метод отличается простотой, однако получаемое с его использованием решение является достаточно приближенным, вследствие чего он в основном применяется для ориентировочных расчетов.
В качестве примера использования метода определим максимальное значение тока в цепи на рис. 1, если 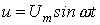 , где
, где 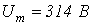 ;
; 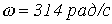 ;
; 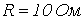 ;
;  . Вебер–амперная характеристика нелинейной катушки индуктивности приведена на рис. 2.
. Вебер–амперная характеристика нелинейной катушки индуктивности приведена на рис. 2.
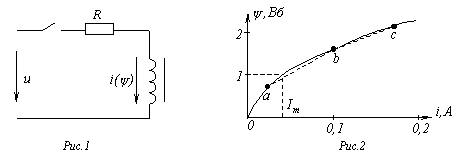
1. Запишем уравнение состояния цепи после коммутации
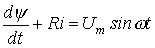 . .
| (1) |
2. Используя метод условной линеаризации, определим второе слагаемое в левой части (1) как
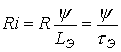 , ,
| (2) |
где 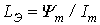 ;
; 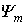 и
и 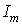 - амплитуды потокосцепления и тока в установившемся послекоммутационном режиме;
- амплитуды потокосцепления и тока в установившемся послекоммутационном режиме; 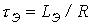 .
.
3. Подставив (2) в (1), получим линейное дифференциальное уравнение
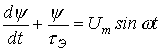 ,
,
решением которого на основании классического метода расчета переходных процессов является
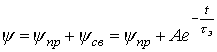 .
.
4. Принужденная составляющая 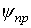 определяется соотношением
определяется соотношением
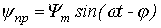 ,
,
где 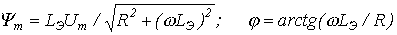 .
.
Для определения 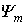 и
и 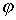 предположим (с последующей проверкой), что
предположим (с последующей проверкой), что 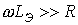 . При этом условии
. При этом условии 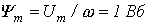 и
и 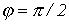 . По зависимости
. По зависимости 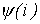 для полученного значения
для полученного значения 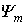 найдем
найдем 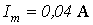 .Тогда
.Тогда 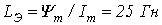 и
и 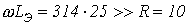 , т.е. сделанное выше предположение корректно.
, т.е. сделанное выше предположение корректно.
Следует отметить, что в общем случае значения 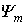 и
и 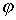 могут быть определены, например, итерационным методом.
могут быть определены, например, итерационным методом.
Определив 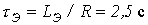 , запишем
, запишем
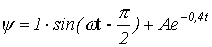 .
.
Поскольку по условию 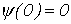 , то
, то 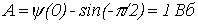 .
.
Таким образом,
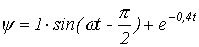 . .
| (3) |
6. Не решая трансцендентное уравнение, будем считать, что максимальное значение потокосцепления имеет место примерно через полпериода своего изменения, т.е. при 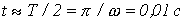 . Подставив это время в (3), получим:
. Подставив это время в (3), получим:
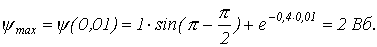
По кривой 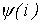 для
для 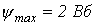 найдем максимальное значение тока
найдем максимальное значение тока 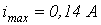 , которое в
, которое в 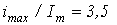 раз превышает амплитуду тока в установившемся послекоммутационном режиме. Напомним, что для линейной цепи
раз превышает амплитуду тока в установившемся послекоммутационном режиме. Напомним, что для линейной цепи 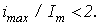
Примечания:1. Обычно при использовании метода условной линеаризации для расчета переходного процесса при подключении нелинейной катушки индуктивности к источнику синусоидального напряжения эквивалентная линейная индуктивность 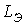 определяется исходя из амплитудных значений тока и потокосцепления в установившемся послекоммутационном режиме, как это и было сделано в рассмотренном выше примере. Однако если необходимо оценить максимально возможное значение тока, то величину индуктивности следует определять по начальному участку вебер–амперной характеристики, где
определяется исходя из амплитудных значений тока и потокосцепления в установившемся послекоммутационном режиме, как это и было сделано в рассмотренном выше примере. Однако если необходимо оценить максимально возможное значение тока, то величину индуктивности следует определять по начальному участку вебер–амперной характеристики, где 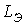 максимальна.
максимальна.
2. Если сопротивление резистора в ветви с нелинейной катушкой достаточно велико, так что 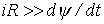 , то следует пренебречь нелинейностью слагаемого
, то следует пренебречь нелинейностью слагаемого 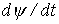 , положив
, положив 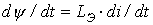 . В этом случае нелинейное уравнение (1) сводится к линейному вида
. В этом случае нелинейное уравнение (1) сводится к линейному вида
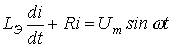 ,
,
и соответственно кривая 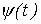 определяется по кривым
определяется по кривым 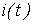 и
и 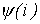 .
.
Дата добавления: 2015-04-19; просмотров: 678;
