Переформированные экспертные оценки
| Кандидаты | Эксперты | Сумма рангов | Средний ранг | |||||||||
| Э1 | Э2 | Э3 | Э4 | Э5 | Э6 | Э7 | Э8 | Э9 | Э10 | |||
| Иванов | 1,5 | 1,5 | 1,6 | |||||||||
| Петров | 1,5 | 1,5 | 2,5 | 4,5 | 3,2 | |||||||
| Сидоров | 5,5 | 4,5 | 4,5 | 34,5 | 3,5 | |||||||
| Смирнов | 3,5 | 4,5 | 2,5 | 32,5 | 3,3 | |||||||
| Федоров | 5,5 | 5,5 | 3,5 | 3,5 | 4,5 | 4,5 | 4,4 | |||||
| Сергеев | 5,5 | 5,5 | 3,5 | 5,5 | 4,5 | 4,5 | 5,1 | |||||
| Число связанных рангов | 3,2 | 2,2 | 2,3 | 2,3 | ||||||||
| Tj |
Здесь вспомогательная величина Tj (j =1, 2,..., 10) рассчитывается по формуле:
Tj = (na3 – na) + (nb3 – nb) + (nc3 – nc) + ...,
где na, nb, nc – количество связанных рангов, образующих группы a, b, с в составе ранжировки, выполненной экспертом j.
Например: Т1 = (33 – 3) + (23 – 2) = 30;
Т6 = (23 – 2) + (23 – 2) + (23 – 2) = 18.
Проверить степень достоверности проведенной экспертизы можно с помощью коэффициента конкордации (т.е. согласованности, от фр. concorde – согласие) W, который показывает, насколько мнения экспертов согласуются друг с другом, то есть принадлежат к одной и той же генеральной совокупности оценок. Величина коэффициента конкордации может меняться в пределах от 0 до 1, причем его равенство единице означает полную согласованность мнений экспертов, а равенство нулю означает, что связи между оценками, полученными от разных экспертов, не существует. В случае, если W < 0,2 – 0,4 говорят о слабой согласованности экспертов, а при W > 0,6 – 0,8 можно говорить о существовании сильной согласованности экспертов. Слабая согласованность обычно является следствием следующих причин:
· в рассматриваемой группе экспертов действительно отсутствует общность мнений;
· внутри группы существуют коалиции с высокой согласованностью мнений, однако обобщенные мнения коалиций противоположны.
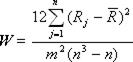 ,
,
где 12 - постоянная величина в формуле расчета коэффициента конкордации, предложенной Кендаллом;
n - число показателей;
m - число экспертов;
Rj- сумма баллов j- го показателя;
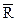 - средняя сумма баллов всех показателей.
- средняя сумма баллов всех показателей.
S = 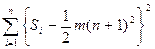 где m – количество экспертов;
n – количество ранжируемых работников;
Si – суммы рангов, расположенные в строках предпоследнего столбца табл. 11.6.
где m – количество экспертов;
n – количество ранжируемых работников;
Si – суммы рангов, расположенные в строках предпоследнего столбца табл. 11.6.
|
Как и обычный коэффициент корреляции, коэффициент W может принимать значения от 0 до 1. В рассматриваемом примере S = 641,5;
Tj = 264.
Подставив все требуемые величины в формулу для расчета коэффициента конкордации, получим: W= 0,466. Значимость коэффициента конкордации проверяют с помощью статистического критерия χ2 ("хи–квадрат"), некоторые значения которого приведены в табл. 11.7.
Таблица 11.7
Значения статистического критерияχ2 приα= 0,05
| n | ||||||||||||
| χ2 | 3,8 | 7,8 | 9,5 | 11,1 | 12,6 | 14,1 | 15,5 | 16,9 | 23,7 | 30,1 | 42,6 |
Коэффициент конкордации значим, и различия в оценках экспертов не существенны, если выполняется неравенство m(n – l)w ≥ χ2.
В нашем случае m(n – l)w = 23,3, что превышает табличное значение χ2 = 11,1. Таким образом, экспертные оценки взаимно непротиворечивы, поэтому их можно усреднить по каждому из шести ранжируемых работников. Результаты усреднения приведены в последнем столбце табл. 11.7. Обобщая результаты, построим гистограмму средних рангов (рис. 11.1).
На последующих этапах организаторами опроса обобщается полученная информация и делаются выводы по ее практическому применению.
Следует помнить, что полученные результаты экспертных оценок не только дают информацию относительно качеств работников, но и позволяют принять решение по их дальнейшему эффективному использованию.
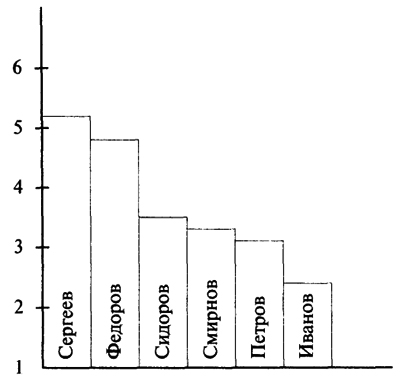
Рис. 11.1. Гистограмма средних рангов
Контрольные вопросы
1. Что такое деловая оценка персонала? Каковы ее задачи?
2. Из каких этапов состоит процесс оценки?
3. Перечислите группы показателей, применяемые в ходе оценки.
4. Охарактеризуйте классификацию методов оценки.
5. От каких факторов зависит коэффициент перспективности работника?
6. Перечислите виды шкал, используемых для оценки.
7. В чем суть ранговой шкалы?
8. С какой целью используется метод ранжирования работников?
9. Приведите примеры качественных методов оценки.
10. Опишите метод критического случая.
11. Какие этапы включает применение метода экспертных оценок?
12. Как скорректировать ранги с помощью переформирования первоначальных данных?
13. Какой коэффициент позволяет проверить наличие связи между двумя показателями деловой оценки?
14. При каком условии коэффициент Спирмена считается статистически значимым?
15. Какой показатель характеризует степень согласованности оценок экспертов?
16. При каком условии можно усреднить оценки экспертов?
17. Какие выводы можно сделать из гистограммы средних рангов?
Дата добавления: 2015-04-19; просмотров: 1680;
