Результаты ранжирования
| Качества руководителей | Ранги, проставленные руководителю № | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Умение работать с персоналом (x) | 5 | |||||||||||
| Чувство личной ответственности за порученное дело (у) |
Для характеристики степени связи между элементами двух ранжировок нельзя использовать обычный коэффициент корреляции, поскольку ранги не являются непрерывными величинами (они дискретны). Вместо этого используют коэффициент ранговой корреляции Спирмена:
ρ = 1 – 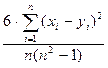 ,
,
где n = 12 (число ранжируемых объектов);
i = 1,2,..., 12, – порядковый номер объекта;
Xi – ранг объекта по свойству x;
Yi – ранг объекта по свойству у.
Подстановка данных ранжирования в эту формулу позволила рассчитать коэффициент ранговой корреляции Спирмена:
ρ = 1 – 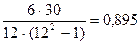
Возможный диапазон этого коэффициента – от 0 до 1. В данном случае он достаточно велик, что говорит о наличии явной связи между сопоставляемыми показателями.
Поскольку экспертные оценки базируются на обработке достаточно субъективных мнений, следует рассматривать их результаты (в том числе и коэффициент ранговой корреляции) как случайные величины. Соответственно коэффициент ρ считают статистически значимым, если выполняется неравенство ρ ≥ ρкр, где ρкр – критическое значение, определяемое по табл. 11.4.
Как и любое статистическое суждение, вывод о величине коэффициента ранговой корреляции необходимо дополнять значением вероятности того, что этот вывод неверен. Эту вероятность называют уровнем значимости, обозначая его греческой буквой а. Естественно стремление к тому, чтобы уровень значимости был приемлемо мал.
Таблица 11.4
Критические значения коэффициента Спирмена при уровне значимостиα= 0,05
| Число ранжируемых объектов (n) | |||||||||
| Критическое значение коэффициента (ρкр) | 0,98 | 0,88 | 0,8 | 0,74 | 0,69 | 0,65 | 0,59 | 0,52 | 0,45 |
В нашем случае n = 12; υкр = 0,59; υ = 0,895 > 0,59, поэтому можно утверждать, что корреляция (соответствие) двух качеств руководителей существенна (статистически значима).
Проверка взаимного соответствия оценок нескольких экспертов. Десять экспертов должны проставить баллы шести работникам, в разной степени обладающим умением анализировать информацию и делать из нее практические выводы. Баллы проставляются таким образом, что минимальный балл по этому качеству составляет 1, максимальный равен 10 (табл. 11.5).
Таблица 11.5
Дата добавления: 2015-04-19; просмотров: 942;
