Работа по перемещению проводника и контура с током в магнитном поле.

При малом перемещении dr элемента dl проводника с током I работа силы Ампера dF равна

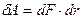
По закону Ампера

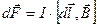
где В — магнитная индукция. Подставляя это выражение в формулу работы, получим

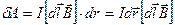
Из векторной алгебры известно, что смешенное произведение трех векторов не измениться, если в нем произвести циклическую перестановку сомножителей.

Поэтому выражение работы можно переписать в виде:

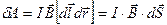(12.8.1)

где 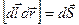— вектор малой площадки dS, прочерчиваемой элементом проводника длиной dl при его малом перемещении dr (рис.12.15.), dФ = BdS — магнитный поток сквозь эту площадку.

Работа А сил Ампера при малом перемещении проводника конечной длины равна сумме элементарных работ сил Ампера для всех малых участков этого проводника, т.е

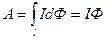, (12.8.2)

магнитный поток сквозь поверхность, прочерченная проводником постоянен по длине проводника только если проводник движется поступательно.

Таким образом, работа, совершаемая силами Ампера при перемещении в магнитном поле проводника, ток в котором постоянен, равна произведению силы тока на магнитный поток сквозь поверхность, которую прочерчивает проводник при своем движении.

Найдем работу сил Ампера при перемещении в магнитном поле замкнутого контура с током I. Пусть в результате малого перемещения контур перешел из положения С в положение С^/ (рис. 12.16.). При этом малый элемент dl контура совершил перемещение dr и прочертил малую площадку dS. Вектор этой площадки 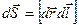показан на рисунке 12.16.

Согласно теореме Остроградского— Гаусса, магнитный поток сквозь нее равен нулю, т.е.

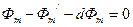
Знак минус перед членом Ф_m взят потому, что при его вычислении использована нормаль n', являющаяся внутренней нормалью к соответствующему участку замкнутой поверхности.

Следовательно, изменение магнитного потока, сцепленного с контуром, происходящее при его малом перемещении определяется выражением

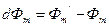(12.8.3)

Интегрируя выражение (12.8.3), найдем работу, совершаемую силами Ампера при перемещении контура с током из начального положения 1 в произвольное конечное положение 2

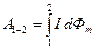
Если в процессе перемещения контура сила тока в нем остается постоянной, то

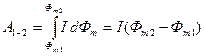(12.8.4)

т.е. работа, совершаемая силами Ампера при перемещении в магнитном поле замкнутого контура, по которому проходит постоянный ток, равна произведению силы тока на изменение магнитного потока сквозь поверхность, ограниченную контуром.

В электротехнике принято обозначать полный магнитный поток через Ψ и называть его потокосцеплением контура (в отличие от магнитного потока сквозь один виток, обозначаемого через Ф_m). Поэтому формулу работу контура, состоящего из N витков записывают в виде

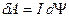(12.8.5)

Потокосцепление контура обусловлено как внешним магнитным полем, так и магнитным полем тока в самом контуре. Если внешнего поля нет, то потокосцепление контура обусловлено только магнитным полем тока в этом контуре и называется потокосцеплением самоиндукции (Ψ_с). Если внешнее магнитное поле создается электрическим током в каком-то контуре, то соответствующее ему потокосцепление другого контура называется потокосцеплением взаимной индукции этих двух контуров.