Закон Архимеда и плавание тел

Пусть тело произвольной формы полностью погружено в жидкость (рис. 17). Выделим цилиндрическую часть этого тела с бесконечно малой площадью поперечного сечения.

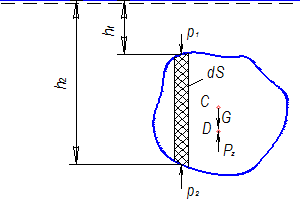
Рис. 17. Гидростатическая подъемная сила

Сила давления, действующая на цилиндрическую часть тела:

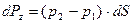, (52)

где	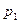,	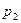- давления, действующие на верхнее и нижнее основания цилиндрика;
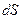
		- площадь верхнего и нижнего оснований цилиндрика.

Из основного закона гидростатики следует

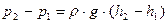, (53)

где	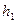,	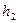- глубина погружения верхнего и нижнего оснований цилиндра;
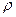
		- плотность жидкости, в которой расположено тело.

Для силы давления, действующей на тело произвольной формы можно написать

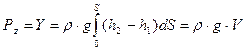, (54)

Полученный результат представляет собой математическое выражение закона Архимеда: на тело, погруженное в жидкость, действует поддерживающая (гидростатическая подъемная) сила, направленная вверх и численно равная силе тяжести вытесненной жидкости.

Точка приложения гиростатической подъемной силы -центр давления (точка D).

Плавание тел в жидкости определяется величиной двух сил: силы тяжести и гидростатической подъемной силы.

Сила тяжести тела

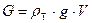, (55)

где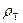

- плотность тела.

Сила тяжести тела приложена в его центре тяжести (точка С), если сила тяжести тела больше гидростатической подъемной силы, то оно тонет, а если 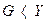- всплывает. Когда эти две силы равны 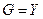, тело плавает на поверхности.