Криволинейную стенку

В отличие от плоской стенки гидростатическое давление в разных точках криволинейной стенки различается не только по величине, но и по направлению. Поэтому силу гидростатического давления, действующую на криволинейную стенку, непосредственно определить нельзя: ее находят через составляющие этого вектора.

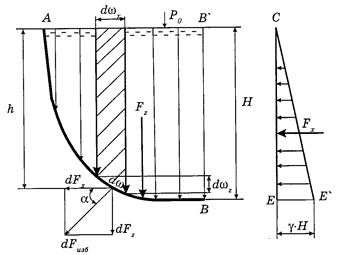
Рис. 15. К определению силы давления на криволинейную стенку

Рассмотрим криволинейную поверхность АВ, подверженную действию избыточного гидростатического давления (жидкость справа) (рис. 15).

Выделим площадку 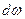, цент тяжести которой погружен в жидкость на глубину 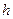. На площадку 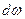будет действовать элементарная сила избыточного давления 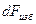нормально ней:

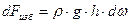, Н (38)

Разложим 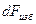на составляющие:

- горизонтальная составляющая силы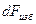

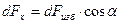, Н (39)

- вертикальная составляющая силы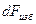

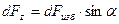, Н . (40)

где 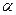- угол составляющей между элементарной площадкой 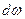и горизонтальной плоскостью, град.

Рассмотрим каждую в отдельную составляющую силы избыточного давления, действующего на криволинейную поверхность АВ.

Элементарная горизонтальная составляющая силы избыточного давления равна

.

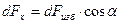В то же время

.

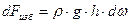Следовательно

.

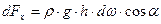Из рис. 15 видно, что

,

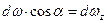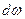где - площадь проекции элементарной площадки на вертикальную плоскость, .

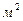Откуда

.

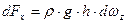Горизонтальная составляющая силы избыточного давления после интегрирования равна

(41)

где 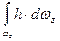- статический момент инерции всей площади проекции 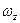относительно свободной поверхности жидкости, ;

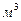т.е. статический момент инерции равен произведению площади вертикальной проекции 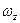на глубину погружения центра ее тяжести .

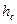Откуда находим

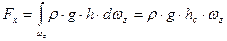(42)

Элементарная вертикальная составляющая силы избыточного гидростатического давления равна:

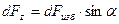, или (43)

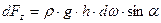
Величина 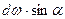является площадью проекции 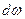на горизонтальную плоскость 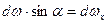. Следовательно

.

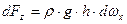Заметим, что 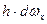представляет собой бесконечно малый объем бесконечно малой призмы, отмеченной на рис. 15 штриховкой.

Произведение 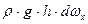является силой тяжести в этом бесконечно малом объеме :

.

Отсюда вертикальная составляющая силы избыточного гидростатического давления будет равна

.

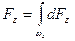После интегрирования находим:

;

;

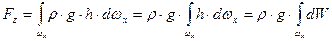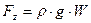. (44)

где 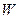- тело давления, .

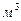Объем 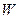, являющийся суммой элементарных объемов, называется телом давления.

Тело давления – это объем, ограниченный криволинейной поверхностью АВ, ее проекцией на уровень свободной поверхности АВ и вертикальными плоскостями проецирования.

Полная сила гидростатического давления определяется из выражения

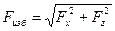(45)

где		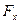- горизонтальная составляющая силы избыточного гидростатического давления, ;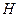
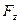
		- вертикальная составляющая силы избыточного гидростатического давления, .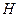

Направление полной силы 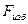определяется углом 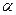(рис. 15):

.

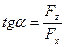Полная сила избыточного гидростатического давления приложена в центре давления.

Вектор полной силы давления 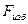должен проходить через точку пересечения ее горизонтальной и вертикальной составляющих, т.е. 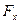и 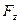под углом .

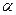Таким образом, цент давления для криволинейных поверхностей находится графоаналитическим путем.

Если криволинейная поверхность цилиндрическая, то сила 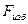будет проходить через центр радиуса кривизны этой поверхности.