В простой замкнутой сети без учета потерь мощности

Представим простую замкнутую сеть в виде линии с двухсторонним питанием (рис.3.9,а) и рассмотрим следующий случай.

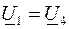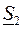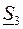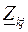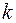Заданы одинаковые напряжения по концам линии . Известны мощности нагрузки , , сопротивления участков линии , где - узел начала участка линии; 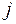- узел конца.

Принимаем следующие допущения: а)пренебрегаем потерями мощности 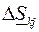при определении потоков 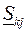; б)предполагаем, что ток участка определяется по номинальному напряжению:

;

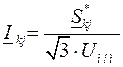в)используем расчетные мощности нагрузок подстанции.

При равенстве напряжений источников питания на основании второго закона Кирхгофа можно записать (рис.3.9,б)

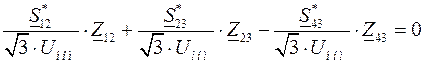. (3.24)

Если заменим в последнем выражении все комплексные величины на сопряженные, то получим следующее уравнение:

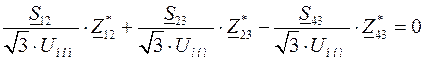. (3.25)

Так как потери мощности не учитываются, первый закон Кирхгофа для узлов 2 и 3 можно записать так:

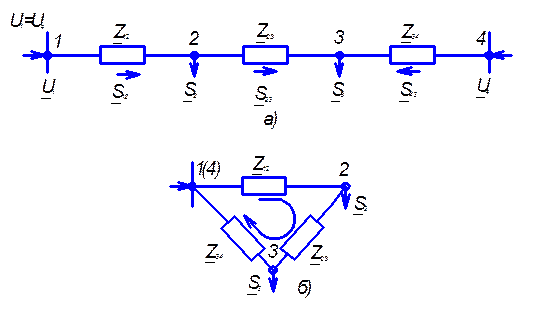
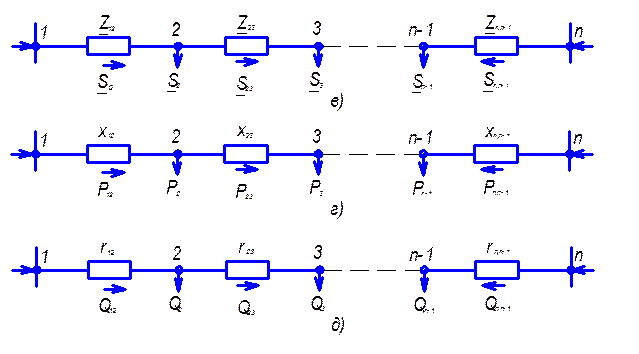
Рис.3.9 Распределение потоков мощности в линии

с двухсторонним питанием без учета потерь мощности:

а – схема замещения линии с четырьмя узлами; б – иллюстрация

второго закона Кирхгофа; в – линия с «n» узлами;

г,д – распределение P и Q в однородной линии.

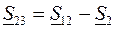; (3.26)

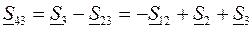. (3.27)

Подставив значения мощностей (3.26) и (3.27) в уравнение (3.25), получим уравнение с одним неизвестным, из которого находим значение потока мощности :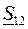

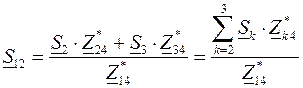, (3.28)

где .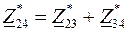

Аналогично можно вывести формулу для определения потока мощности :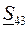

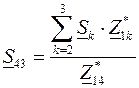, (3.29)

где .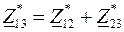

Значение потока мощности 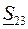можно легко найти на основании первого закона Кирхгофа из (3.26).

Рассмотрим линию с количеством узлов, равным 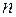(рис.3.9,в). Потоки мощности на головных участках определятся так:

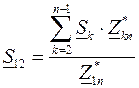, (3.30)

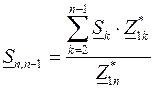. (3.31)

Если известны токи нагрузок 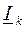, то можно определить токи на головных участках линии аналогично (3.30), (3.31):

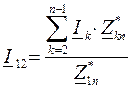; (3.32)

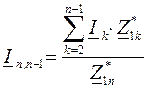. (3.33)

В однородной сети отношение активного и реактивного сопротивлений всех ветвей схемы замещения сети одинаково:

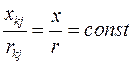, (3.34)

поэтому формулу (3.30) для однородной сети можно записать в виде

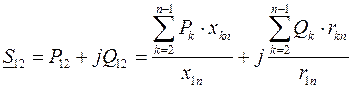. (3.30а)

Аналогично для однородной сети из (3.31) можно получить следующее выражение:

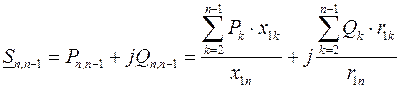. (3.31а)

В однородной сети, все участки которой выполнены проводами (кабелями) одного сечения с удельными активным и реактивным сопротивлениями 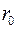, , 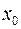распределение мощностей можно находить по длинам участков, поскольку сопротивление каждой ветви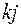

.

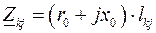При одинаковом сечении проводов вдоль всей линии формулы (3.30) и (3.31) принимают вид

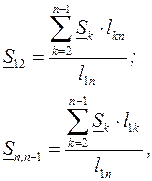(3.35)

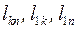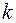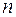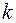где - длины участков линии между узлами соответственно и , 1 и , 1 и .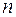

Вышеприведенные формулы показывают, что в однородных сетях распределение активных и реактивных мощностей (токов) не зависит друг от друга. Нахождение распределения 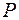и 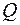в таких сетях упрощается, при этом лучшие результаты получают в сетях с отношением 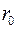/ 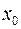<1 при распределении активных мощностей по соотношению индуктивных сопротивлений, а реактивных мощностей по соотношению активных сопротивлений. Рассчитываются как бы две независимые сети: одна – нагруженная только активными нагрузками (рис.3.9,г) и вторая – реактивными (рис.3.9,д). Для каждой из них определяется распределение мощностей. По схеме рис.3.9,г определяется распределение активных мощностей, а по схеме рис.3.9,д – реактивных. Полные мощности на участках сети (рис.3.9,в) находятся суммированием проходящих по ним активных и реактивных мощностей. Такой расчетный прием, называемый расщеплением сети, уменьшает трудоемкость расчета сети.

Следует обратить внимание на то, что равенство сечений проводов на всех участках сети не позволяет считать сеть однородной. Нужно, чтобы и удельные реактивные сопротивления линий на всех участках сети были также равными.

Сеть, один участок которой выполнен кабелем, а другой - воздушной линией, даже при равных сечениях проводов и жил кабелей и выполнении их из одного и того же металла не будет однородной. Неоднородной будет и воздушная сеть, по всей длине которой подвешены одни и те же провода, но с неодинаковым среднегеометрическим расстоянием между ними на разных участках сети. В обоих случаях при равенстве удельных активных сопротивлений участков линии удельные реактивные сопротивления будут не равны.

Искусственными мерами сеть с неодинаковыми сечениями и расположением проводов на разных участках можно сделать однородной. Достигается это последовательным включением конденсатора на некоторых участках сети; сопротивления конденсаторных батарей берутся такими, чтобы отношения активного и реактивного сопротивлений отдельных участков сети стали одинаковыми. В результате можно в некоторых случаях снизить потери мощности и электроэнергии в сети и улучшить режим напряжения у потребителей.