Нормирование метрологических характеристик чувствительности средств измерений к влияющим величинам.

Влияние, оказываемоевнешними факторами, описывается при помощи следующих характеристик.

Функция влияния ψ(ξ) — это зависимость изменения МХ средства измерений от изменения влияющей величины или их совокупности в рабочих условиях применения СИ. Использование функций влияния позволяет определить не предельно возможные значения погрешности, практически не встречающиеся при исправных СИ, а их статистические оценки. Нормирование функции производится путем установления ее номинального значения и пределов допустимых отклонений от него. Возможно нормирование граничных, верхней и нижней функций влияния.

Изменения значений метрологических характеристик СИ, вызванные изменениями влияющих величин в установленных пределах, ε(ξ)— это разность (без учета знака) между МХ, соответствующей некоторому заданному значению влияющей величины ξ в пределах рабочих условий применения СИ, и данной МХ, соответствующей нормальному значению влияющей величины. Эти изменения нормируются путем установления пределов допускаемых изменений характеристики при изменении влияющей величины в заданных пределах.

Дополнительная погрешность СИ вызывается изменениями влияющих величин относительно своих нормальных значений и, следовательно, является ихфункцией. Для различных экземпляров СИ одного типа могут значительно меняться как вид функции, так и ее параметры. Однако для всех СИ того или иного типа эти функции должны быть подобны, а их параметры близки. Поэтому в качестве основной характеристики дополнительной погрешности принята некоторая средняя (номинальная) для данного типа функция зависимости погрешности от изменения влияющих величин.

Функции влияния могут нормироваться как отдельно для каждой влияющей величины, так и для определенной их совокупности. Нормирование совместных функций целесообразно и необходимо в тех случаях, когда существенны эффекты взаимовлияния величины на характеристики погрешностей.

Влияющие величины могут вызывать изменения не только погрешности, но и других МХ средства измерений. Поэтому для таких случаев целесообразно предусмотреть нормирование соответствующих функций влияния.

Функция ψ(ξ) устанавливает связь между статистическими характеристиками дополнительной погрешности Δ_С СИ и изменением влияющей величины: Δξ = ξ – ξ₀, где

ξ и ξ₀ — текущее значение влияющей величины в реальных условиях применения СИ и ее нормированное значение соответственно. Математическое ожидание (систематическая составляющая) и СКО дополнительной погрешности имеют вид: М[Δ_С] = ψ_ΔS(ξ);

σ[Δ_C] = ψ₀(ξ), где ψ_ΔS(ξ) и ψ₀(ξ) - функции влияния величины ξ на систематическую погрешность и СКО случайной погрешности СИ. При необходимости функция влияния на вариацию нормируется отдельно. В этом случае характеристики погрешности конкретного СИ выражаются следующим образом (для простоты считается, что вариация равна нулю):

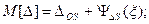
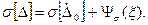
Данные формулы справедливы в том случае, когда изменения влияющих величин Δξявляются известными детерминированными функциями. Если же Δξ учитываются как случайные величины или функции, обладающие своими математическими ожиданиями и дисперсиями, то последние формулы должны быть записаны в виде

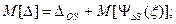
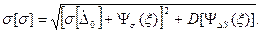
Это особенно важно для функции влияния ψ_ΔS(ξ) поскольку влияющие величины обычно вызывают значительные изменения именно систематической погрешности. В данном случае функция влияния ψ_ΔS(ξ) характеризуется своим математическим ожиданием М[ψ_ΔS(ξ)] и дисперсией D[ψ_ΔS(ξ)].

Учет влияния случайного разброса величин Δξ на дисперсию или СКО, путем введения соответствующих функций ψ_D(ξ) и ψ_σ(ξ), привел бы к тому, что их необходимо было бы учитывать как случайные величины. И поэтому сама случайная погрешность СИ должна была бы рассматриваться как случайная функция с очень сложным видом нестационарности. Все это привело бы к практически непреодолимым трудностям при оценке погрешностей. В то же время значения Δξ влияют на характеристики случайной погрешности значительно меньше, чем на систематическую погрешность. Этот дает основание пренебречь влиянием разброса величин Δξ на дисперсию случайной погрешности и рассматривать функции влияния ψ_D(ξ) и ψ_σ(ξ) как детерминированные. При проведении расчетов рекомендуется учитывать только те значения аргументов Δξ, при которых данные функции влияния имеют максимальные значения — ψ_σ(ξ)_max.

Для функции влияния нормируются ее вид и параметры. Характеристики аргумента Δξ при расчетах определяются исходя из реальных условий эксплуатации СИ. При этом знания только предельных значений Δξ недостаточно. Необходимо иметь информацию как о центре группирования, так и о степени ее разброса.

Функции влияния могут иметь самый разный вид. В простейшем случае они являются линейными: ψ_ΔS(ξ) = A Δξ, где A – постоянная величина. В этом случае

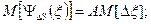
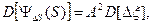где M[Δξ] и D[Δξ] – математическое ожидание и дисперсия величины Δξ соответственно.

Наиболее просто дополнительные погрешности рассчитываются для СИ, у которых функции влияния различных внешних величин (температуры, влажности, напряжения питания и т.д.) взаимно независимы.На практике возможны ситуации, когда имеет место взаимная зависимость функций влияния нескольких величин ξ_1, ξ₂, …, ξ_L. В этом случае нормируют функцию совместного влияния ψ(ξ_1, ξ₂, …, ξ_L), которая и используется при расчетах дополнительной погрешности.

Неинформативные параметры выходного сигнала являются одним из видов влияющих величин и определяют допустимую область значений тех параметров выходного сигнала, которые не содержат непосредственной информации о значении измеряемой величины. Однако они определяют возможность нормальной работы СИ.

Неинформативные параметры выходного сигнала СИ нормируют путем установления номинальных значений и пределов допускаемых отклонений от них.