Прямой.
Смещение тела, участвующего одновременно в двух или нескольких колебаниях, находится на основании принципа суперпозиции, согласно которому эти колебания накладываются, не влияя одно на другое.
Пусть материальная точка участвует в двух гармонических колебаниях, направленных вдоль одной прямой, круговые частоты этих колебаний одинаковы, а начальные фазы различны. Такие колебания описываются уравнениями:
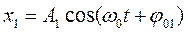
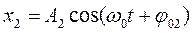
При сложении колебаний направленных по одной прямой результирующее смещение точки в любой момент времени равно сумме смещений, которые точка имела бы в каждом из колебаний в отдельности в тот же момент времени:
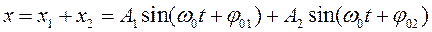
Такое сложение значительно облегчается, если использовать метод векторной диаграммы. Векторной диаграммой называется графическое изображение колебаний в виде векторов на плоскости (рис. 2.4.).
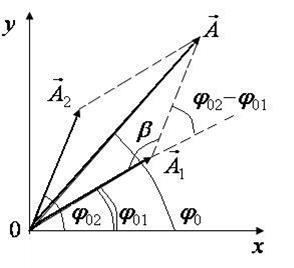 Рис. 2.4.
Рис. 2.4.
|
На плоскости 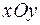 из точки
из точки 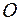 отложим под углом
отложим под углом 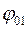 к оси
к оси 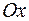 вектор
вектор 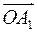 , длина которого равна амплитуде первого колебания
, длина которого равна амплитуде первого колебания 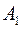 . Из точки
. Из точки 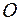 отложим под углом
отложим под углом 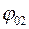 к оси
к оси 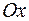 вектор
вектор 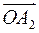 , длина которого равна амплитуде второго колебания
, длина которого равна амплитуде второго колебания 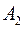 . Проекция векторов
. Проекция векторов 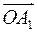 и
и 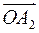 на ось
на ось 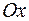 равна соответственно смещению
равна соответственно смещению 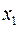 и
и 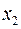 . Если привести векторы
. Если привести векторы 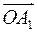 и
и 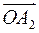 во вращение с круговой частотой
во вращение с круговой частотой 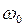 , то смещения
, то смещения 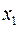 и
и 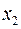 будут изменяться по гармоническому закону. Сложим векторы
будут изменяться по гармоническому закону. Сложим векторы 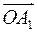 и
и 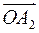 геометрически по правилу параллелограмма. Результатом сложения является вектор
геометрически по правилу параллелограмма. Результатом сложения является вектор 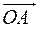 длина которого равна амплитуде результирующего колебания. Проекция этого вектора на ось
длина которого равна амплитуде результирующего колебания. Проекция этого вектора на ось 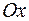 равна сумме проекций слагаемых векторов:
равна сумме проекций слагаемых векторов: 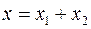 . Следовательно, вектор
. Следовательно, вектор 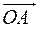 представляет собой результирующее гармоническое колебание
представляет собой результирующее гармоническое колебание
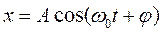
Амплитуда результирующего колебания
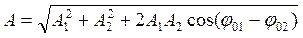
Частные случаи:
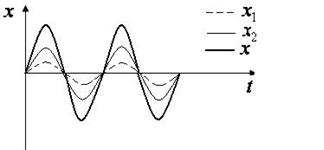 1) если
1) если 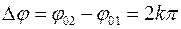 , где
, где 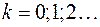 , то амплитуда результирующего колебания равна
, то амплитуда результирующего колебания равна
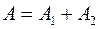
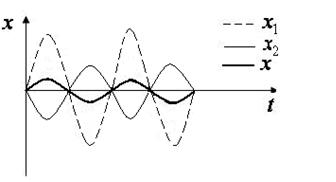
2) если 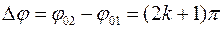 где
где 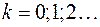 , то амплитуда результирующего колебания равна
, то амплитуда результирующего колебания равна 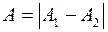
Дата добавления: 2015-04-19; просмотров: 1314;
