График. Логарифмический декремент затухания.
В природе все происходящие колебания реальные, т.е. при их рассмотрении нельзя пренебрегать силой трения: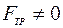 . На преодоление силы трения расходуется полная механическая энергия колеблющегося тела. Поэтому с течением времени амплитуда колебаний уменьшается до нуля, колебания прекращаются и тело возвращается в положение равновесия.
. На преодоление силы трения расходуется полная механическая энергия колеблющегося тела. Поэтому с течением времени амплитуда колебаний уменьшается до нуля, колебания прекращаются и тело возвращается в положение равновесия.
Затухающие колебания материальной точки происходят под действием двух сил: возвращающей силы 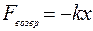 и силы трения
и силы трения 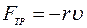 , где
, где 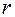 - коэффициент трения,
- коэффициент трения, 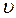 - скорость.
- скорость.
Уравнение движения колеблющегося тела в векторной форме:
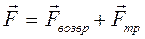
уравнение движения в скалярной форме:
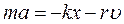
Дифференциальное уравнение затухающих колебаний:
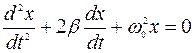 ,
,
где 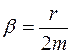 - коэффициент затухания.
- коэффициент затухания.
Решение дифференциального уравнения:
 или
или 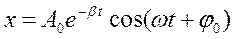 ,
,
где 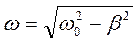 - круговая частота колебаний, при
- круговая частота колебаний, при 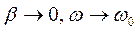 .
.
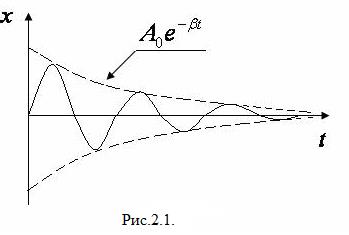
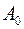 - начальная амплитуда колебаний.
- начальная амплитуда колебаний.
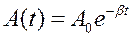 - амплитуда затухающего колебания.
- амплитуда затухающего колебания.
Период затухающих колебаний: 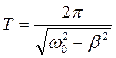
График затухающих колебаний (рис.2.1). На практике степень затухания характеризуют логарифмическим декрементом затухания, который показывает в логарифмическом масштабе во сколько раз амплитуда в любой момент времени 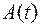 больше амплитуды через период
больше амплитуды через период 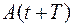 .
.
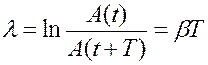
Дата добавления: 2015-04-19; просмотров: 2586;
