Тема 5.
ГИДРОДИНАМИКА
Гидродинамика - раздел физики, в котором изучается движение несжимаемых жидкостей. Законы гидродинамики позволяют описать движение крови по сосудам.
Идеальная жидкость - жидкость несжимаемая и не имеющая внутреннего трения или вязкости.
Стационарное или установившееся течение - течение, при котором скорости частиц жидкости в каждой точке потока со временем не изменяются.
Установившееся течение характеризуют линиями тока.
Линии тока - это воображаемые линии, совпадающие с траекториями движения частиц.
Трубка тока - часть потока жидкости, ограниченная со всех сторон линиями тока.
Уравнение неразрывности струи
В общем потоке жидкости выделяют трубку тока настолько узкую, что скорость частиц в любом её сечении, перпендикулярном оси трубки, можно считать постоянной: в сечении 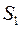 скорость -
скорость - 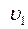 , в сечении
, в сечении 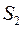 скорость -
скорость - 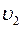 (рис.5.1).
(рис.5.1).
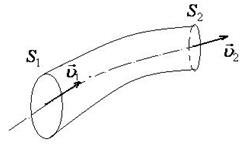 Рис. 5.1.
Рис. 5.1.
|
При стационарном течении частицы движутся только по линиям тока, поэтому боковую поверхность они не пересекают. Если за время 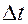 в трубку тока вошел объём жидкости
в трубку тока вошел объём жидкости 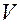 , то такой же объём жидкости должен и выйти из неё. поэтому
, то такой же объём жидкости должен и выйти из неё. поэтому
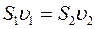 , т.е.
, т.е. 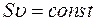 -
-
уравнение неразрывности струи: при установившемся течении по трубе переменного сечения количество жидкости, протекающее в единицу времени через любое поперечное сечение трубы, остается постоянным.
Уравнение Бернулли
Рассмотрим течение идеальной жидкости по трубе переменного сечения. Выделим в потоке идеальной жидкости трубку тока, а в ней достаточно малый объем жидкости 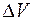 , массой
, массой 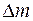 , который при течении жидкости перемещается из положения 1 в положение 2 (рис. 5.2.).
, который при течении жидкости перемещается из положения 1 в положение 2 (рис. 5.2.). 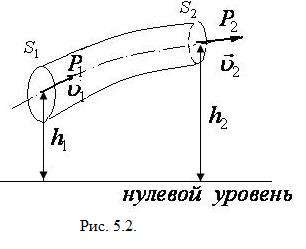
Жидкость, находящаяся под давлением, обладает внутренней потенциальной энергией 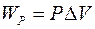 ,
,
где 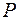 – давление.
– давление.
При перемещении жидкости совершается работа:
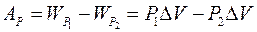
Эта работа расходуется на преодоление действия сил тяжести: работа 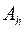 , и на изменение кинетической энергии жидкости: работа
, и на изменение кинетической энергии жидкости: работа 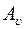 :
:
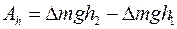 ,
,
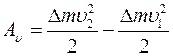 .
.
Уравнение Бернулли: 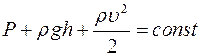 ,
,
где 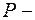 статическое давление,
статическое давление, 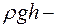 гидростатическое давление,
гидростатическое давление, 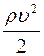 - гидродинамическое давление. Уравнение Бернулли: полное давление жидкости, равное сумме статического, гидростатического и гидродинамического давлений, остается постоянным в любом сечении трубы.
- гидродинамическое давление. Уравнение Бернулли: полное давление жидкости, равное сумме статического, гидростатического и гидродинамического давлений, остается постоянным в любом сечении трубы.
Практические следствия из уравнения Бернулли.
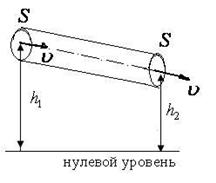 Рис. 5.3. Рис. 5.3.
|
Определение гидростатического давления. Рассматривают трубу тока постоянного сечения площадью 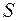 (рис. 5.3.), высота сечений над нулевым уровнем энергии различна и равна
(рис. 5.3.), высота сечений над нулевым уровнем энергии различна и равна 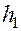 и
и 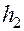 , соответственно. Т.к. площадь сечений одинакова, то скорость течения жидкости и гидродинамическое давление остается величиной постоянной. Уравнение Бернулли принимает вид
, соответственно. Т.к. площадь сечений одинакова, то скорость течения жидкости и гидродинамическое давление остается величиной постоянной. Уравнение Бернулли принимает вид
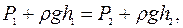
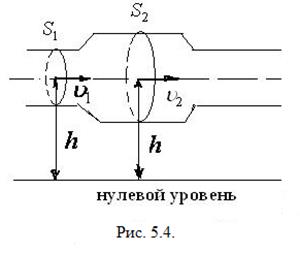 Следовательно
Следовательно 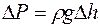 .
. 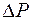 измеряют манометром и определяют перепад гидростатического давления на данном участке трубы.
измеряют манометром и определяют перепад гидростатического давления на данном участке трубы.
Правило Бернулли. Выбирают горизонтальную трубу, имеющую различные сечения 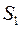 и
и 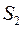 (рис. 5.4.), следовательно, скорости
(рис. 5.4.), следовательно, скорости 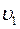 и
и 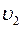 также разные (
также разные ( 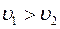 ), гидростатическое давление остается постоянным. Уравнение Бернулли принимает вид
), гидростатическое давление остается постоянным. Уравнение Бернулли принимает вид
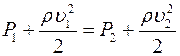 , или
, или 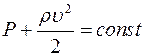
Правило Бернулли: статическое давление невязкой жидкости при течении по горизонтальной трубе возрастает там, где скорость ее уменьшается, и наоборот.
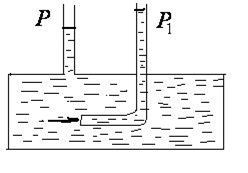 Рис. 5.5. Рис. 5.5.
|
Определение гидродинамического давления и скорости течения жидкости.Выберем горизонтальную трубку тока постоянного сечения, уравнение Бернулли запишется в виде
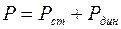 , где
, где 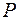 - полное давление, тогда
- полное давление, тогда 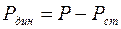 . Статическое давление жидкости
. Статическое давление жидкости 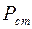 измеряют при помощи манометрической трубки, плоскость отверстия которой расположена параллельно движению жидкости. Для измерения полного давления применяют манометрическую трубку, изогнутую под прямым углом навстречу движения жидкости. Зная
измеряют при помощи манометрической трубки, плоскость отверстия которой расположена параллельно движению жидкости. Для измерения полного давления применяют манометрическую трубку, изогнутую под прямым углом навстречу движения жидкости. Зная 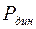 можно определить скорость течения жидкости:
можно определить скорость течения жидкости: 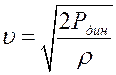 .
.
Вязкость жидкости.
При течении реальной жидкости между молекулами действуют силы взаимного притяжения, в результате чего возникает внутреннее трение (вязкость).
Формула Ньютона: 
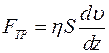 , где
, где 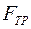 - сила внутреннего трения между двумя слоями жидкости, она ускоряет медленно текущие слои и замедляет быстротекущие слои, направлена сила трения по касательной к поверхности соприкасающихся слоев;
- сила внутреннего трения между двумя слоями жидкости, она ускоряет медленно текущие слои и замедляет быстротекущие слои, направлена сила трения по касательной к поверхности соприкасающихся слоев; 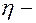 коэффициент внутреннего трения (коэффициент вязкости),
коэффициент внутреннего трения (коэффициент вязкости), 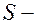 площадь соприкосновения слоёв,
площадь соприкосновения слоёв, 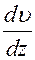 - градиент скорости
- градиент скорости 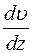
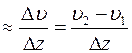 - показывает на сколько изменяется скорость при изменении толщины слоя на единицу.
- показывает на сколько изменяется скорость при изменении толщины слоя на единицу. 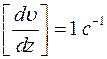

Физический смысл коэффициента внутреннего трения: 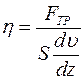 -коэффициент внутреннего трения показывает, какая сила трения возникает при соприкосновении слоев на площади, равной 1 м2, при градиенте скорости между ними, равном 1 с-1.
-коэффициент внутреннего трения показывает, какая сила трения возникает при соприкосновении слоев на площади, равной 1 м2, при градиенте скорости между ними, равном 1 с-1.

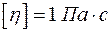
Внесистемной единицей является 1 Пуаз; 1 П = 0,1 Па ·с
Ламинарное и турбулентное течение
Ламинарное течение – течение, при котором слои жидкости движутся параллельно друг другу не смешиваясь между собой. Ламинарное течение наблюдается при небольших скоростях течения в трубках с гладкими стенками, без резких изменений площади сечения и без разветвлений.
Турбулентное течение – течение, при котором слои жидкости перемешиваются, образуя вихри. Скорости молекул жидкости беспорядочно меняются, молекулы жидкости переходят из слоя в слой, за счет этого происходит перемешивание жидкости. Турбулентное течение сопровождается шумами.
Характер течения жидкости определяется числом Рейнольдса
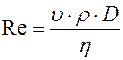 ,
,
где 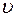 - скорость течения жидкости,
- скорость течения жидкости, 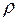 - плотность жидкости,
- плотность жидкости, 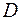 - диаметр трубы,
- диаметр трубы, 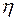 - вязкость жидкости.
- вязкость жидкости.
Существует критическое число Рейнольдса ( 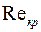 ). Если
). Если 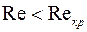 возможно только ламинарное течение, если
возможно только ламинарное течение, если 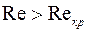 возможно только турбулентное течение. Для однородной жидкости критическое число Рейнольдса
возможно только турбулентное течение. Для однородной жидкости критическое число Рейнольдса
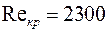 , для крови -
, для крови - 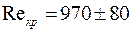 (в зависимости от диаметра сосуда).
(в зависимости от диаметра сосуда).
Распределение скорости и градиента по сечению
трубы при ламинарном течении.
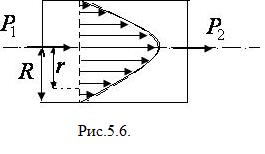 Рассмотрим ламинарное течение вязкой жидкости по горизонтальной трубе постоянного сечения (рис. 5.6.). Распределение скорости по сечению трубы носит параболический характер:
Рассмотрим ламинарное течение вязкой жидкости по горизонтальной трубе постоянного сечения (рис. 5.6.). Распределение скорости по сечению трубы носит параболический характер:
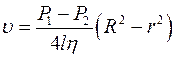 ,
,
где 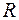 - радиус трубы,
- радиус трубы, 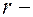 радиус рассматриваемого слоя,
радиус рассматриваемого слоя, 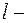 длина трубы,
длина трубы, 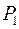 и
и 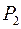 – давление в начале и конце трубы, соответственно.
– давление в начале и конце трубы, соответственно.
Скорость имеет наибольшее значение в центре трубы:
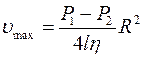 ,
, 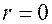 .
.
Градиент скорости максимален в пристеночной части трубы:
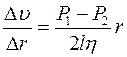 .
.
Течение реальной жидкости по горизонтальной трубе постоянного сечения. Закон Гагена - Пуазейля.
При течении жидкости по горизонтальной трубе постоянного сечения (рис. 5.7.) потенциальная энергия её частиц расходуется на работу по преодолению внутреннего трения. Поэтому статическое давление вдоль трубы постепенно падает. Высота 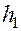 соответствует начальному статическому давлению, а высота
соответствует начальному статическому давлению, а высота 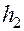 – гидродинамическому давлению, обеспечивающему скорость течения жидкости. Крутизна этой кривой (тангенс угла наклона) характеризует продольный градиент давления:
– гидродинамическому давлению, обеспечивающему скорость течения жидкости. Крутизна этой кривой (тангенс угла наклона) характеризует продольный градиент давления: 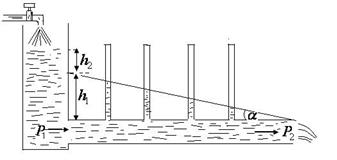
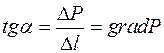 .
.
Рис.5.7. Пуазейль определил среднюю скорость течения жидкости по горизонтальной трубе постоянного сечения: 
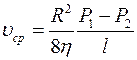 – закон Пуазейля. Количество жидкости, протекающей через поперечное сечение за единицу времени
– закон Пуазейля. Количество жидкости, протекающей через поперечное сечение за единицу времени
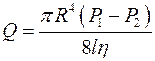 - закон Гагена-Пуазейля.
- закон Гагена-Пуазейля.
Течение жидкости по горизонтальной трубе переменного сечения
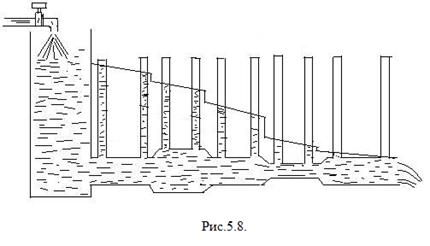
Средняя скорость течения зависит от радиуса трубы 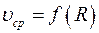 . Поэтому на участках трубы различного сечения скорости различны. По правилу Бернулли статическое давление невязкой жидкости при течении по горизонтальной трубе увеличивается там, где скорость её уменьшается, и наоборот. Кроме того, в местах изменения сечения трубы течение становится турбулентным, что вызывает потери энергии. Кроме того, поскольку количество жидкости, протекающее через поперечное сечение, не меняется, то меняется градиент давлений: при переходе от меньшего сечения к большему давление падает меньше, а при переходе от большего сечения к меньшему давление падает больше.
. Поэтому на участках трубы различного сечения скорости различны. По правилу Бернулли статическое давление невязкой жидкости при течении по горизонтальной трубе увеличивается там, где скорость её уменьшается, и наоборот. Кроме того, в местах изменения сечения трубы течение становится турбулентным, что вызывает потери энергии. Кроме того, поскольку количество жидкости, протекающее через поперечное сечение, не меняется, то меняется градиент давлений: при переходе от меньшего сечения к большему давление падает меньше, а при переходе от большего сечения к меньшему давление падает больше.
Течение жидкости по разветвленной трубе
В разветвленной трубе градиент давлений зависит:
1) от общего сечения разветвленной части, т.к. от этого зависит средняя скорость течения жидкости, и, следовательно, общие потери энергии.
2) от числа труб в разветвленной части, т.к. в разветвленной части площадь пристеночных слоев велика, то и потери энергии большие.
Чем больше трубок, тем больше потери энергии, тем больше падает давление.
Течение жидкости по трубе с эластичными стенками
Если жидкость течет по эластичной трубе, то упругие свойства материала стенок влияют на характер течения жидкости. При поступлении жидкости в трубу труба растягивается, а затем, сжимаясь, проталкивает жидкость силой обратной деформации.
Контрольные вопросы
•Основные понятия: свойства и особенности молекулярного строения жидкостей. Идеальная жидкость. Стационарное течение, линии тока, трубка тока. •Уравнение неразрывности струи. Уравнение Бернулли. •Практические следствия из уравнения Бернулли. •Внутреннее трение. Формула Ньютона. Смысл градиента скорости. Коэффициент внутреннего трения. Относительная и кинематическая вязкости. •Ламинарное и турбулентное течение жидкости. Число Рейнольдса. •Течение жидкости по горизонтальной трубе постоянного сечения. Закон Гагена-Пуазейля. •Течение жидкости по горизонтальной трубе переменного сечения, по разветвленной и по трубе с эластичными стенками.
Тема 6.
БИОРЕОЛОГИЯ.
Биореология - раздел физики, изучающий течение биологических жидкостей, обладающих вязкостью и пластичных.
 У некоторых жидкостей, преимущественно высокомолекулярных, коэффициент вязкости зависит не только от температуры и природы жидкости, но и от режима течения, градиента скорости, давления и др. факторов. Такие жидкости называются неньютоновскими к которым относится и кровь. В качестве примера неньютоновских жидкостей кровь. В биореологии формула Ньютона записывается в форме:
У некоторых жидкостей, преимущественно высокомолекулярных, коэффициент вязкости зависит не только от температуры и природы жидкости, но и от режима течения, градиента скорости, давления и др. факторов. Такие жидкости называются неньютоновскими к которым относится и кровь. В качестве примера неньютоновских жидкостей кровь. В биореологии формула Ньютона записывается в форме:
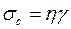 ,
,
где 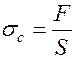 - напряжение сдвига,
- напряжение сдвига, 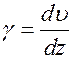 - скорость сдвига.
- скорость сдвига.
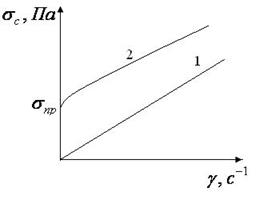
Кривые течения – графики зависимости напряжения сдвига от скорости сдвига.
| Рис. 6.1. |
На рис. 6.1. кривая 1 соответствует ньютоновской жидкости. Кривая 2 соответствует неньютоновской жидкости, т.е. вязко-пластичной жидкости. Здесь жидкость начинает течь только при 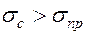 , где
, где 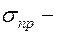 предел текучести.
предел текучести.
Зависимость коэффициента вязкости крови
от различных физических факторов.
Зависимость вязкости крови от градиента скорости.
С увеличением скорости сдвига (рис. 6.2.), т.е. с увеличением 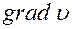 , эффективная вязкость крови резко падает и при γ > 100 с-1 вязкость крови становится равной некоторому предельному значению, остающемуся далее неизменным как у ньютоновской жидкости. Это происходит оттого, что агрегаты эритроцитов с увеличением градиента скорости распадаются, следовательно, кровь находится под напряжением
, эффективная вязкость крови резко падает и при γ > 100 с-1 вязкость крови становится равной некоторому предельному значению, остающемуся далее неизменным как у ньютоновской жидкости. Это происходит оттого, что агрегаты эритроцитов с увеличением градиента скорости распадаются, следовательно, кровь находится под напряжением 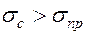 . 1 –эффективная вязкость, 2 – коэффициент вязкости ньютоновской жидкости.
. 1 –эффективная вязкость, 2 – коэффициент вязкости ньютоновской жидкости.
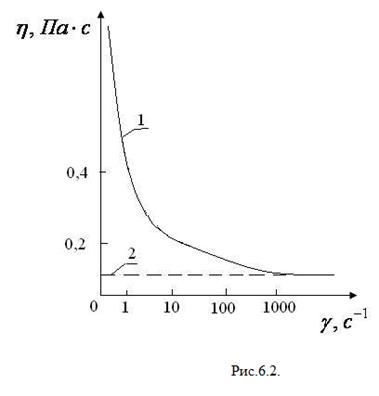
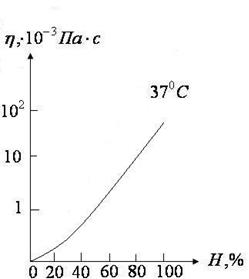
Рис. 6.3.
Зависимость вязкости крови от гематокритного показателя 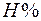 ,
,
т.е. от концентрации эритроцитов в крови. С увеличением гематокритного показателя вязкость крови возрастает (рис. 6.3.), т.к. увеличивается число комплексов и увеличиваются их размеры.
Зависимость вязкости крови от температуры
С увеличением температуры вязкость уменьшается, т.к. уменьшаются силы взаимодействия между молекулами эритроцитов, уменьшаются размеры агрегатов. В пределах температур от 10 0С до 380С вязкость крови имеет экспоненциальную зависимость от температуры
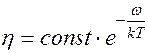
При температурах меньше 100С и выше 380С зависимость очень сложная, что связано с процессами, приводящими к изменению свойств крови.
Зависимость вязкости крови от диаметра сосуда, по которому течет кровь (рис.6.4.).
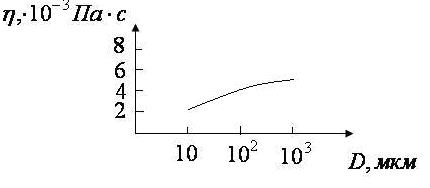 С увеличением диаметра сосуда вязкость крови увеличивается. В сосудах диаметром меньше 50 мкм этот эффект проявляется столь сильно, что может маскировать зависимость вязкости крови от скорости сдвига
С увеличением диаметра сосуда вязкость крови увеличивается. В сосудах диаметром меньше 50 мкм этот эффект проявляется столь сильно, что может маскировать зависимость вязкости крови от скорости сдвига
| Рис. 6.4. |
Физические модели кровообращения.
Гидродинамическая модель
| а) | б) | в) |
| 
| 
|
Рис. 6.5.
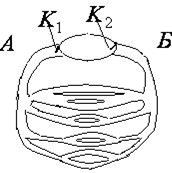
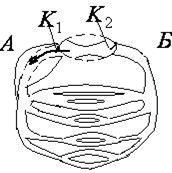
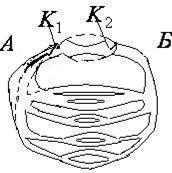
Модель представлена в виде замкнутой системы трубок с эластичными стенками (рис.6.5.). Эта система заполнена жидкостью. Движение жидкости в ней происходит под действием ритмично работающего насоса в виде груши. Широкие трубки – аналог аорты и артерий, резкие разветвления – аналог периферической системы – капилляров.
Электрическая модель. 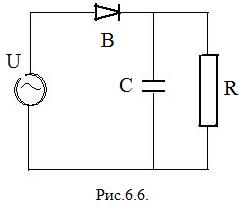 На рис. 6.6:
На рис. 6.6: 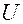 - источник переменного несинусоидального переменного напряжения, который служит аналогом сердца. Выпрямитель (диод)
- источник переменного несинусоидального переменного напряжения, который служит аналогом сердца. Выпрямитель (диод) 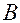 , пропускающий ток только в одном направлении, служит аналогом клапана. Конденсатор
, пропускающий ток только в одном направлении, служит аналогом клапана. Конденсатор 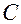 служит аналогом упругого резервуара (аорты и артерий).
служит аналогом упругого резервуара (аорты и артерий).
Конденсатор служит для накопления заряда. Участки упругих резервуаров (аорта, артерии), обладающие эластичностью, можно рассматривать как емкость для крови. Вязкостное сопротивление, большее у периферических сосудов, можно представить в виде резистора 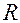 .
.
Закономерности выброса и распространения крови
в большом круге кровообращения.
При каждом сокращении левого желудочка сердца в аорту, уже заполненную кровью под соответствующим давлением, выталкиваться некоторый объем крови, называемый ударным объёмом ( 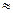 65 – 70 мл). Затем сердечный клапан закрывается.
65 – 70 мл). Затем сердечный клапан закрывается.
Волна повышенного давления, называемого систолическим, вызывает колебания сосудистых стенок. Волна повышенного давления, вызванная выбросом крови из левого желудочка во время систолы, называется пульсовой волной. Скорость пульсовой волны 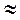 5 – 10 м/c.
5 – 10 м/c.
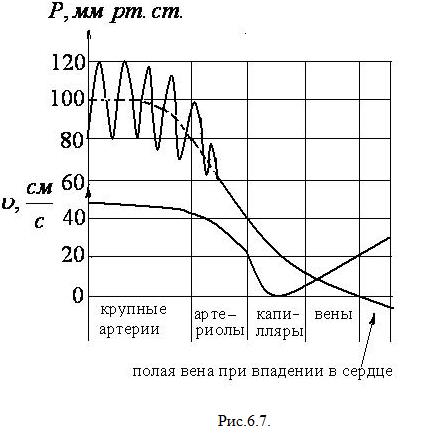
Сопротивление току крови и падение давления на разных участках сосудистой системы различны (рис. 6.7.). Оно зависит от общего сечения (общего просвета) и от числа сосудов в разветвлении. Наибольшее падение происходит в артериолах (до 50 % от начального). Это связано с тем, что число артериол в сотни раз больше, чем крупных артерий при сравнительно небольшом увеличении общего просвета сосудов. Поэтому потери давления от пристеночного трения достаточно большие. Общее число капилляров ещё больше, поэтому даже при небольшой их длине их падение давления в них значительно, но меньше, чем в артериолах.
В венах падение давления незначительно. Это связано с тем, что площадь сечения венозных сосудов в среднем в 2 раза больше, чем в артериях. Имеется участок, в котором давление оказывается ниже атмосферного. Этот участок соответствует движению крови под влиянием присасывающего действия грудной клетки при вдохе.
На рис.6.7. представлен также график изменения скорости крови при прохождении её по разным сосудам. Как видим из рисунка в артериях скорость крови постоянна. В артериолах она падает и в капиллярах становится равной нулю. В венах скорость крови повышается.
Работа и мощность сердца.
Работа, совершаемая сердцем, складывается в основном из работы при сокращении желудочков сердца, главным образом левого желудочка. Работа правого желудочка равна 0,15 –0,2 АЛ.Ж..
Работа сердечной мышцы при каждом сокращении левого желудочка затрачивается на сообщение объёму выталкиваемой крови энергии, необходимой для его продвижения по всему кругу кровообращения. Эта энергия состоит из потенциальной энергии давления и кинетической энергии для сообщения массе крови необходимой скорости движения:
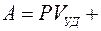
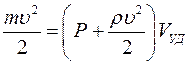
где 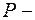 среднее давление, под которым кровь проталкивается в аорту (
среднее давление, под которым кровь проталкивается в аорту ( 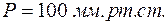 );
); 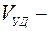 ударный объём крови (
ударный объём крови ( 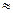 70 мл);
70 мл); 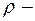 плотность крови (1,05·103 кг/м3);
плотность крови (1,05·103 кг/м3); 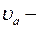 скорость крови в аорте (
скорость крови в аорте ( 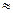 0,5 м/с в состоянии покоя)
0,5 м/с в состоянии покоя)
Работа левого желудочка: 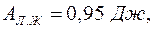 а работа сердца
а работа сердца
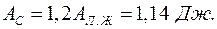 Время сокращения желудочков
Время сокращения желудочков 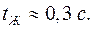 Тогда мощность сердца, развиваемая за одно сокращение
Тогда мощность сердца, развиваемая за одно сокращение 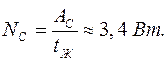
Контрольные вопросы
•Ньютоновские и неньютоновские жидкости. •Аналогия внутреннего трения с деформацией сдвига. Формула Ньютона в биореологии. Кривые течения. •Зависимость вязкости крови от различных факторов (градиента скорости, гематокритного показателя, температуры, диаметра сосуда). Эффективная и кажущаяся вязкости. •Модели кровообращения (гидродинамическая и электрическая). •Закономерности выброса и распространения крови в большом круге кровообращения. Ударный объем крови, пульсовая волна. Распределение давления и скорости кровотока в большом круге кровообращения.• Работа и мощность сердца.
Тема 7.
БИОЛОГИЧЕСКИЕ МЕМБРАНЫ
Значение и функции биологических мембран. Строение мембран.
Структурной и функциональной единицей живого организма является клетка, которой присущи все основные жизненные функции. Мембраны окружают всю цитоплазму и отграничивают её от окружающей среды. Проникновение веществ в клетку и из клетки в большей степени зависит от свойств мембран. Мембраны находятся и внутри клетки, образуя оболочки всех органоидов и включений клетки.
Согласно модели Даниэлли и Давсона основу мембраны составляют два слоя фосфолипидов. Молекула фосфолипида имеет полярную “головку” и неполярный “хвост”. Два слоя молекул фосфолипидов расположены перпендикулярно поверхности мембраны (рис. 7.1). Гидрофильные концы молекул (полярные головки)
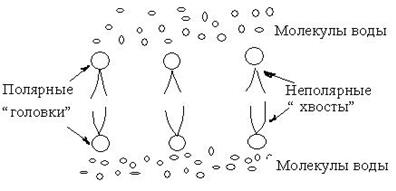
Рис.7.1
способны взаимодействовать с дипольными молекулами воды и формировать гидратные оболочки. Поэтому гидрофильные концы молекул липидов направлены наружу мембраны. Гидрофобные (неполярные) концы молекул направлены вглубь мембраны.
В настоящее время наибольшее распространение получила жидкомозаичная модель, предложенная в 1972 году Синджером и Никольсоном. В основе этой модели лежит также двухслойная липидная мембрана (рис. 7.2). Эта фосфолипидная основа представляет собой как бы двумерный растворитель, в котором плавают более или менее погруженные белки
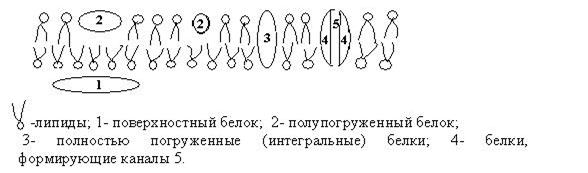
Рис.7.2
Физиологические функции мембран.
•Делят клетку на отдельные участки, в которых протекают различные биохимические реакции. •Принимают участие во всех процессах обмена веществ, которые обусловливают жизнедеятельность клетки. •Координируют и регулируют биохимические и биофизические процессы в клетках. •Клеточные мембраны обеспечивают адгезию (сцепление) клеток друг с другом, что обеспечивает существование ткани.
Физические свойства мембран.
1. Фосфолипиды в мембране находятся в жидкокристаллическом состоянии.
2. Вязкость липидного слоя мембраны на 2 порядка (в 100 раз) выше, чем у воды.
3. Коэффициент поверхностного натяжения липидного слоя на 2-3 порядка (100-1000 раз) меньше, чем у воды. Значит, поверхностная энергия липидного слоя незначительна, что облегчает диффузию веществ через мембрану.
4. При изменении температуры в мембране наблюдаются фазовые переходы.
5. Двойной фосфолипидный слой уподобляет мембрану конденсатору. Электроёмкость участка мембраны площадью в 1 мм2 составляет 5-13 нФ.
Модели искусственных мембран для изучения свойств мембран.
1. Частокол Ленгмюра (рис 7.3) – монослой фосфолипидов. На поверхность воды наносят каплю растворенных в каком-либо растворителе фосфолипидов или 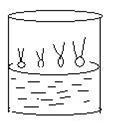 жирных кислот. После распределения их молекул на поверхности воды и испарения растворителя на поверхности воды остается пленка. Адсорбированные молекулы липидов располагаются перпендикулярноповерхности воды.
жирных кислот. После распределения их молекул на поверхности воды и испарения растворителя на поверхности воды остается пленка. Адсорбированные молекулы липидов располагаются перпендикулярноповерхности воды.
Рис. 7.3
2. 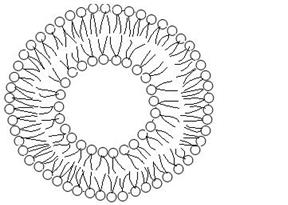 Липосомы (рис. 7.4)– широко распространенная модель. Это мельчайшие пузырьки, состоящие из билипидной мембраны. Получаются при обработке смеси воды и фосфолипидов ультразвуком.
Липосомы (рис. 7.4)– широко распространенная модель. Это мельчайшие пузырьки, состоящие из билипидной мембраны. Получаются при обработке смеси воды и фосфолипидов ультразвуком.
Билипидная мембрана. Берут два водных раствора, разделенных тефлоновой перегородкой с отверстием. Отверстие заполняют фосфолипидом, растворенным в гексане. Когда растворитель и излишек
Рис.7.4
липида растекаются по тефлону, в отверстии образуется бислой толщиной в несколько нанометров.
Методы исследования мембран
1. Микрокалориметрия.
Изучаются фазовые переходы на каком-либо участке мембраны и оценивают число молекул, участвующем в фазовом переходе. Энтропия 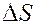 возрастает с ростом длины углеводородной цепи жирных кислот, причем на каждую метиленовую группу приходится примерно постоянное увеличение энтропии при фазовом переходе. Таким образом, можно судить о длине углеводородной цепи липидов.
возрастает с ростом длины углеводородной цепи жирных кислот, причем на каждую метиленовую группу приходится примерно постоянное увеличение энтропии при фазовом переходе. Таким образом, можно судить о длине углеводородной цепи липидов.
2. ИК - спектроскопия.
Этот метод основан на том, что молекулы каждого вещества имеют индивидуальные, специфические спектры поглощения. Молекулярные спектры позволяют исследовать состав мембран, строение молекул в мембране и характер межмолекулярных взаимодействий.
3. Люминесцентный анализ.
Для исследования мембран к мембранным системам добавляют флюоресцирующие молекулы: флуоресцентные зонды, если молекула образует нековалентную связь с мембраной, или флюоресцентные метки, если молекула образует химическую связь с мембраной.
4. Рентгеноструктурный анализ.
В основе этого метода лежит дифракция рентгеновского излучения на структуре мембран. Т.к. липиды мембраны есть жидкий кристалл, то дифракционная картина непосредственно связана с внутренней структурой кристалла. Рентгеноструктурный анализ позволяет определить строение и параметры липидных молекул.
5.Электронный парамагнитный резонанс (ЭПР).
Если атом находится в постоянном магнитном поле, то переходы между подуровнями одного и того же уровня маловероятны. Но если на атом подействовать внешним переменным магнитным полем таким, что частота этого поля 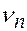 совпадет с частотой фотона, энергия которого равна
совпадет с частотой фотона, энергия которого равна 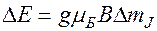 , переходы становятся возможными. При этом происходит поглощение или излучение электронным парамагнитным резонансом (ЭПР).
, переходы становятся возможными. При этом происходит поглощение или излучение электронным парамагнитным резонансом (ЭПР).
В медико-биологических исследованиях с помощью метода ЭПР обнаруживают и исследуют свободные радикалы. По спектрам ЭПР объяснили механизм образования свободных радикалов при радиационном поражении; изучают канцерогенную активность некоторых веществ; изучают фотосинтез.
Для изучения биологических молекул используют метод спин-меток, при котором в различные части молекул исследуемого вещества вводится спин-метка – парамагнитная молекула с хорошо изученной структурой, которая образует ковалентную связь с исследуемым веществом. По изменению спектра спин-метки можно установить расположение различных групп атомов, их взаимодействия, изучать природу и ориентацию химических связей, обнаруживать молекулярное движение.
Дата добавления: 2015-04-19; просмотров: 3748;
