Обобщенная градиентная аппроксимация

Проблема же недостаточной точности приближения LDA приводит к тому, что молекулярные связи, вычисляемые при оптимизации геометрии, оказываются слишком короткими. Для решения этой проблемы может использоваться обобщенная градиентная аппроксимация (generalized gradient approximation, GGA).

Помимо значения локальной электронной плотности, она использует также градиент плотности в точке. Таким образом, GGA можно считать следующим порядком приближения по сравнению с LDA.

Корреляционный функционал GGA записывается в виде:

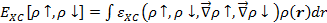. (3.29)

Вообще говоря, GGA — это семейство методов, которые являются полуэмпирическими. Например, в методе PBE обменная энергия записывается как

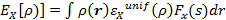, (3.30)

где 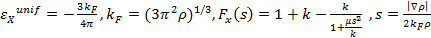(3.31)

k=0.804 и m=0.21951 - эмпирические коэффициенты.

8-й учебный вопрос: Функционал Беке

Другим вариантом полуэмпирического GGA приближения является функционал Беке:

,

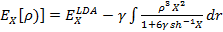Где 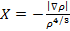,, а g=0.0042— эмпирический параметр, подбираемый так, чтобы воспроизвести обменные энергии атомов инертных газов.

Обычно корреляционный потенциал вычисляется из значений электронной плотности на некоторой конечной сетке, соответственно градиент вычисляется с использованием конечно-разностных формул.

Конечная сетка строится как набор сферических оболочек вокруг каждого атома, каждая из которых содержит набор точек для разностной схемы. Сетки могут быть равномерными и неравномерными (усеченными). В первом случае на каждой сфере содержится одинаковое число точек, во втором используется более редкая сетка в местах, где для достижения необходимой точности достаточно меньшего числа точек.

То есть усеченные сетки строятся так, чтобы быть наиболее плотными в областях, в которых свойства меняются наиболее быстро.

Существуют и более точные приближения, которые в значительной степени позволяют решить проблему вычисления функционала обменно-корреляционной энергии. Локальные методы типа GGA и LDA не всегда дают точность, достаточную для химических вычислений. В настоящее время разрабатываются более точные полуэмпирические методы (meta GGA, MGGA).

В частности, одним из направлений улучшения метода является добавление нелокальной информации в подынтегральное выражение.

На практике метод Кона — Шэма может быть применён несколькими различными способами в зависимости от цели исследования. В расчётах для физики твёрдого тела до сих пор широко используется приближение локальной плотности вкупе с базисом плоских волн. Для расчётов электронной структуры молекул требуются более сложные выражения для функционалов. Так, большое число приближенных функционалов для расчёта обменно-корреляционного взаимодействия было развито для задач химии. Некоторые из них противоречат приближению пространственно однородного электронного газа, тем не

менее, в пределе при переходе к электронному газу должны сводиться к приближению локальной плотности.

Для расчётов физических задач наиболее часто применяется уточнённая обменная модель PBE, однако известно, что она приводит к ошибкам в калориметрических параметрах, будучи приложенной к расчётам молекул в газовой фазе.