Импульс. Закон сохранения импульса.

Импульсом принято называть величину .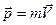

Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокуп­ность материальных точек (тел), рассмат­риваемых как единое целое, называется механической системой.Силы взаимодей­ствия между материальными точками ме­ханической системы называются внутрен­ними.Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними.Механическая система тел, на которую не действуют внешние силы, называется замкнутой(или изолированной).Если мы имеем механиче­скую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направле­ны, т. е. геометрическая сумма внутренних сил равна нулю.

Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны т₁, m₂, . .., т_n и 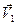, , 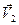.. ., 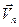. Пусть 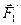, , 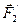..., 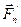— равнодействующие внутренних сил, действующих на каждое из этих тел, a 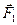, , 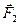..., 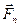— равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:

,

,

………………

.

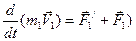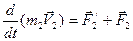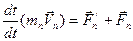Складывая почленно эти уравнения, получим

.

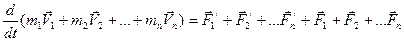Но так как геометрическая сумма внутрен­них сил механической системы по третьему закону Ньютона равна нулю, то

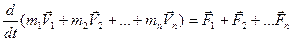
или

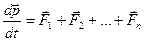(2-4)

где 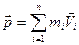импульс системы. Таким образом, производная по времени от им­пульса механической системы равна гео­метрической сумме внешних сил, действующих на систему.

В случае отсутствия внешних сил (рассматриваем замкнутую систему)

.

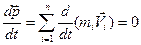т.е. 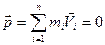. (2-5)

Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.